Способы записи алгоритмов - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 8 КЛАССЕ

Планируемые образовательные результаты:

• предметные — знание различных способов записи алгоритмов;

• метапредметные — умение анализировать предлагаемые последовательности команд на предмет наличия у них таких свойств алгоритма, как дискретность, определенность, понятность, результативность, массовость; понимание преимущества и недостатков той или иной формы записи алгоритмов; умение переходить от одной формы записи алгоритмов к другой; умение выбирать форму записи алгоритма, соответствующую решаемой задаче;

• личностные — алгоритмическое мышление, необходимое для профессиональной деятельности в современном обществе.

Решаемые учебные задачи:

1) закрепление понятий “алгоритм”, “исполнитель”, “свойства алгоритма”;

2) рассмотрение словесных способов записи алгоритмов;

3) рассмотрение графического способа записи алгоритмов с помощью блок-схем;

4) формирование общих представлений об алгоритмических языках.

Основные понятия, рассматриваемые на уроке:

• алгоритм;

• словесное описание;

• построчная запись;

• блок-схема;

• школьный алгоритмический язык.

Средства ИКТ, используемые на уроке:

• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;

• ПК учащихся.

Электронное приложение к учебнику:

• презентация “Способы записи алгоритмов”.

Свободное программное обеспечение:

1) система КуМир — Комплект учебных миров (http://www.niisi.ru/kumir/);

2) редактор блок-схем (http://viktor-zin.blogspot.ru/2011/09/blog-post_5556.html).

Особенности изложения содержания темы урока

После проверки домашнего задания ученикам можно предложить обсудить следующие ситуации:

Задание 1 (базовый уровень). Человек находится в лабиринте и начинает двигаться в направлении, указанном стрелкой, согласно следующему предписанию: идти шаг за шагом, не отрывая руки от правой стены; шагать, пока не выйдешь из лабиринта.

Почему данное предписание нельзя считать алгоритмом выхода из лабиринта? Какое свойство алгоритма здесь нарушено?

1) Определенность

2) Понятность

3) Результативность

4) Массовость

Ответ: 3.

Задание 2 (базовый уровень). Исполнитель Вычислитель выполняет следующую последовательность действий:

1) переменной s присвоить значение 0;

2) переменной i присвоить значение 1;

3) если i > 10, то перейти к выполнению п. 6; иначе выполнить п. 4;

4) увеличить значение переменной s на i;

5) увеличить значение переменной i на 1;

6) сообщить значение s.

Каким свойством не обладает данная последовательность действий?

1) Дискретность

2) Определенность

3) Результативность

4) Массовость

Ответ: 4.

Задание 3 (базовый уровень). Исполнитель Вычислитель работает с числами, записанными на доске. Он может:

• подсчитывать количество чисел на доске;

• сравнивать количество имеющихся на доске чисел с 1;

• находить сумму любых двух чисел, стирать с доски эти числа, увеличивать эту сумму на 1 и записывать на доске полученный результат.

Пока на доске более одного числа, Вычислитель стирает любые два из них и вместо них записывает их сумму, увеличенную на единицу. Каким свойством не обладает последовательность действий, совершаемая исполнителем?

1) Определенность

2) Понятность

3) Результативность

4) Массовость

Ответ: 1.

При изложении нового материала особое внимание уделяется правилам построения блок-схем. Можно продемонстрировать ученикам работу редактора блок-схем и в дальнейшем активно его использовать.

Домашнее задание

§ 2.2; вопросы и задания № 1-8 к параграфу, № 103 в РТ.

Дополнительное задание: № 9 к параграфу.

Указания, комментарии, ответы и решения

Задания в учебнике

№ 4. См. комментарий к № 111 в РТ.

№ 5. См. комментарий к № 112 в РТ.

№ 6. См. комментарий к № 113 в РТ.

№ 8

Задания в рабочей тетради

№ 111. Для сложения двух обыкновенных дробей а/b и c/d нужно привести их к общему знаменателю b ∙ d, для чего числитель первой дроби умножить на знаменатель второй дроби, а числитель второй дроби умножить на знаменатель первой дроби, т. е. а ∙ d, с ∙ b. Полученные результаты сложить (а ∙ d + b ∙ с) и считать числителем результата. Знаменателем результата считать b ∙ d.

№ 112. Алгоритм взвешиваний:

1) сравнить по весу первую пару арбузов,

2) сравнить по весу вторую пару арбузов;

3) сравнить более тяжелый арбуз из первой пары с более тяжелым арбузом из второй пары — это позволит найти самый тяжелый арбуз;

4) сравнить более легкий арбуз из первой пары с более легким арбузом из второй пары — это позволит найти самый легкий арбуз;

5) сравнить два оставшихся арбуза — в зависимости от результатов взвешивания они получат 2-е и 3-е места.

№ 113

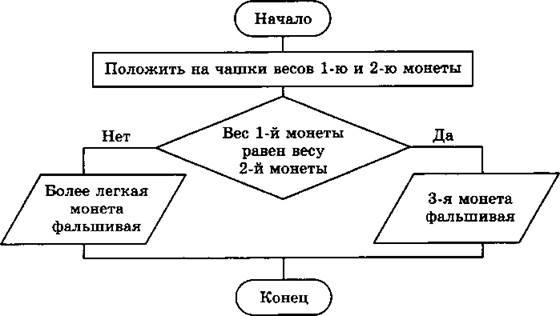
№ 114