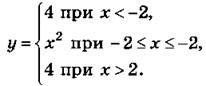Программирование разветвляющихся алгоритмов. Условный оператор. Составной оператор. Многообразие способов записи ветвлений - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 8 КЛАССЕ

Планируемые образовательные результаты:

• предметные — умение записывать на языке программирования короткие алгоритмы, содержащие алгоритмическую конструкцию “ветвление”;

• метапредметные — умение самостоятельно планировать пути достижения целей; умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи;

• личностные — алгоритмическое мышление, необходимое для профессиональной деятельности в современном обществе; представление о программировании как сфере возможной профессиональной деятельности.

Решаемые учебные задачи:

1) рассмотреть правила записи условного оператора;

2) рассмотреть формат и назначение составного оператора;

3) подвести учащихся к выводу, что для решения одной и той же задачи можно разработать разные алгоритмы;

4) сформировать умение записывать на языке программирования короткие алгоритмы с ветвлениями.

Основные понятия, рассматриваемые на уроках:

• условный оператор;

• неполная форма условного оператора;

• составной оператор;

• вложенные ветвления.

Средства ИКТ, используемые на уроках:

• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;

• ПК учащихся.

Электронное приложение к учебнику:

• презентация “Программирование разветвляющихся алгоритмов”.

Особенности изложения содержания темы уроков

Эти два урока — уроки-практикумы. Большое количество заданий в учебнике и рабочей тетради позволят учителю организовать выполнение заданий по группам на разном уровне сложности. Важно, чтобы ученики понимали математическую постановку задачи и суть тех алгоритмов, которые они программируют.

На первом уроке в обязательном порядке следует рассмотреть № 180, 181 в РТ, примеры 1 и 2 на с. 129-130 учебника, где на уже знакомых ученикам алгоритмах демонстрируется использование условного и неполного условного операторов. Далее следует предложить ученикам самостоятельно написать программу по № 140 и выполнить № 143 в РТ. Дополнительно более сильным ученикам можно предложить выполнить задание № 7 в учебнике (с использованием неполного условного оператора).

На втором уроке рекомендуется рассмотреть конструкцию составного оператора. Рассматривается пример из учебника — программа решения квадратного уравнения; обсуждаются с учениками задания № 3, 5 в учебнике; для самостоятельного выполнения на компьютере предлагаются № 184 в РТ, № 11 к § 3.4 учебника.

Очень важно обратить внимание учеников на то, что можно использовать разные варианты записи ветвлений; рассмотреть вложенные ветвления. При изложении этого материала можно опираться на примеры из учебника (с. 131-132). Далее следует обратить внимание на возможные сложности с использованием вложенных ветвлений (задание № 12 в учебнике). После этого можно обсудить с учениками вариант использования вложенных ветвлений в программе определения принадлежности точки отрезку (отказываемся от составного условия). Наиболее сильным ученикам можно предложить использовать вложенные ветвления в программах из заданий № 7 и 8 в учебнике.

Задания № 13, 14 и 15 к § 3.4 учебника, № 187 в РТ можно рекомендовать для самостоятельного выполнения более сильным ученикам.

При изучении этой и других тем по программированию можно рекомендовать проведение занятий по модели “перевернутого урока”.

Принято считать, что на “традиционном” уроке, который длится 45 минут, школьники в основном слушают учителя, делают записи и, в редких случаях, задают вопросы. В конце урока они получают домашнее задание, чтобы закрепить учебный материал. Дома школьники пытаются разобраться с заданиями, но часто сталкиваются с трудностями, и на следующем занятии приходится повторять изученный материал. При таком подходе учитель по-прежнему занимает ведущую, руководящую позицию в учебной ситуации, которая заключается в основном в передаче информации, контроле знаний и в удержании дисциплины на уроке. При организации “перевернутого обучения” ученики дома смотрят и слушают подготовленные для них материалы. Затем приходят на занятие в школу, объединяются в группы и решают задачи, делают практические задания, задают вопросы друг другу и педагогу, при этом они сами обучают и поддерживают друг друга. В процессе консультирования и наблюдения за школьниками педагог понимает, насколько усвоен материал, и двигается дальше.

Далее представлен возможный сценарий перевернутого урока информатики в 8 классе по теме “Условный оператор”. Урок входит в курс уроков по программированию на языке Паскаль. Школьники знакомы с общими сведениями о языке программирования Паскаль, с организацией ввода и вывода данных, умеют программировать линейные алгоритмы.

После того как обучающиеся продуктивно поработали на уроке, посвященном различным типам данных, в качестве домашнего задания они получают видеоматериал, выложенный на странице:http://infourok.ru/arhiv/pascal/pascal.html, и возможность самостоятельно изучить пункты 1 и 2 параграфа 3.4 “Программирование разветвляющихся алгоритмов” учебника информатики для 8 класса и ЭОР к данному параграфу.

Занятия проходят один раз в неделю, поэтому у школьников есть время подготовиться к уроку дома или в любой день недели после уроков в школьном компьютерном классе, где можно в свободное время посмотреть видеоматериал и ЭОР.

В начале урока целесообразно повторить со школьниками следующие вопросы:

— Что входит в состав алфавита языка Паскаль?

— Каких требований следует придерживаться при выборе имен для различных объектов в языке Паскаль и какие типы данных он использует?

— Какую структуру имеет программа, записанная на языке Паскаль?

— Какие операторы используются для ввода и вывода данных?

После этого следует перейти к изучению новой темы “Программирование разветвляющихся алгоритмов” и начать ее изучение с темы “Условный оператор”.

Далее учителю следует убедиться, что все ученики изучили дома новый материал.

Чтобы это проверить, учитель предлагает записать на доске общий вид условного оператора. Он вызывает произвольного ученика к доске, тот записывает:

Следующий ученик записывает неполную форму условного оператора:

Далее учитель может попросить ученика разъяснить, что означают ключевые слова в данной записи: if — then — else, как они переводятся на русский язык.

Еще один ученик объясняет, как оформить контейнер из нескольких операторов, и уточняет, когда операторные скобки begin и end являются обязательными, а когда их можно опустить.

Следующий ученик должен ответить, когда и где надо ставить знак “точка с запятой”, и уточнить, что перед else знак “;” не ставится.

Основная задача учителя на данном этапе — опросить как можно большее количество обучающихся, тем самым вовлечь их всех в учебную деятельность.

Еще один ученик должен написать на доске программу, согласно которой можно определить принадлежность точки х отрезку [А, В].

Школьники определяют, все ли верно записал на доске их одноклассник. Если потребуется, то одноклассники должны внести коррективы.

Следующим шагом школьникам предлагается написать на доске программу нахождения наибольшего из трех чисел.

После этого педагог может быть уверен, что школьники усвоили материал из учебника.

Затем целесообразно перейти к программе, которая будет находить корни квадратного уравнения. Именно эта программа была разобрана в видеофрагменте.

Для начала все школьники в тетради записывают квадратное уравнение в общем виде, учитель может сделать это на доске и задать вопрос классу:

— Какие переменные нужны для решения данной задачи и какой у них может быть тип?

— Как начать программу и как описать переменные?

Один из учеников класса выходит к доске и делает первые записи.

Далее преподаватель спрашивает:

— Как получить коэффициенты уравнения а, b, с?

Следующий ученик записывает на доске операторы ввода для указанных переменных.

Еще один школьник записывает на доске вычисление дискриминанта квадратного уравнения на языке Паскаль.

Далее ученики рассуждают о количестве корней в квадратном уравнении. Один из них записывает блок операторов для случая, когда дискриминант равен нулю.

Следующий школьник пишет на доске блок операторов для случая, когда дискриминант меньше нуля. И наконец, еще один ученик записывает блок операторов для нахождения двух корней квадратного уравнения и проговаривает, в каком это будет случае.

Попутно надо вспомнить, как записываются функции возведения в квадрат и извлечения квадратного корня.

Результатом работы учеников под руководством учителя будет программа решения квадратного уравнения.

Можно предложить ученикам еще раз внимательно посмотреть на программу и обсудить, всё ли верно в ней написано. Если ошибок в программе нет, то надо перейти к процессу сокращения программного кода. Из программы требуется убрать лишние слова begin и end. Обязательно нужно вспомнить, что перед else не должно быть точки с запятой. Это делают сами обучающиеся. Учитель наблюдает.

Когда программный код сокращен, можно перейти к работе на компьютерах и предложить школьникам набрать готовую программу в среде языка Паскаль. Для проверки правильности программы ученикам можно предложить решить три уравнения:

2х² + 5x + 25 = 0;

х² + 2х + 1 = 0;

2х² + 2х - 12 = 0.

В первом уравнении дискриминант меньше нуля, поэтому уравнение не имеет корней, именно такой вариант ответа школьники должны увидеть у себя на экране.

Во втором уравнении дискриминант равен нулю, поэтому уравнение имеет один корень, х = -1.

В третьем случае школьники должны получить в качестве ответа два корня квадратного уравнения: х = 2 и х = -3.

На этом этапе основная цель занятия достигнута. Школьники усвоили, что такое условный оператор, при этом учитель в процессе занятия ничего сам не объяснял. Ученики самостоятельно выясняли и писали на доске все элементы нового материала. Даже если кто-то из обучающихся пришел на урок неподготовленным (по каким-то причинам не смог прочитать и просмотреть новый материал), то, прослушав и просмотрев все, что делали и объясняли его одноклассники, он разберется в новой теме. Это станет окончательно ясно, если он правильно наберет программу для решения квадратного уравнения и получит верные решения для трех предложенных уравнений.

Следующим этапом урока должна стать самостоятельная работа обучающихся. Им можно предложить задания из учебника или отдельные задания на карточках. Учитель в это время наблюдает за работой учеников и помогает в написании программы тем, кто испытывает затруднения.

В конце урока учитель подводит итоги и дает новое домашнее задание.

Домашнее задание

Урок 1: § 3.4 (пункт 1); вопросы и задания № 1, 2, 6а, 9 к параграфу; задание № 182 в РТ. Урок 2: § 3.4 (пункты 2-3); № 16 к параграфу, задания № 185, 186 в РТ.

Дополнительное задание: № 10 к параграфу.

Указания, комментарии, ответы и решения

Задания в учебнике

№ 3

а) Да;

б) нет;

в) нет.

№ 5

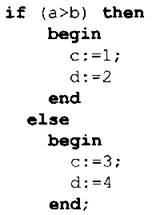
№ 6

№ 7. Вначале рекомендуется построить чертеж:

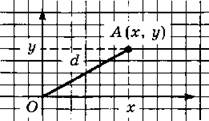
№ 8

№ 9. Делается по аналогии с примером нахождения наибольшей из трех величин (пример 9 в пункте 2.4.2 параграфа 2.4 учебника).

№ 10. Здесь также важно понимание математической сути задачи. Можно предложить ученикам выполнить соответствующие построения в тетради и выяснить положение заданных точек относительно заданной прямой. После этого уже следует сформулировать общее правило и на его основании написать программу.

№ 11. Воспользуемся универсальным алгоритмом обмена значениями двух переменных с использованием промежуточной переменной. Соответствующий алгоритм описан на с. 66 учебника (пример 2).

Для решения этой задачи можно запрограммировать и алгоритм обмена значениями числовых величин и без промежуточной переменной:

№ 12. а = 5. Для ответа на вопрос рекомендуется построить фрагмент блок-схемы.

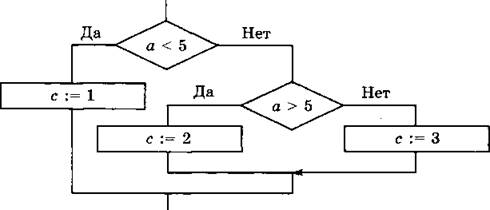
№ 13. Важно, чтобы ученики понимали смысл аналитической записи функции, а именно могли по аналитической записи построить график функции и блок-схему соответствующего алгоритма.

№ 14

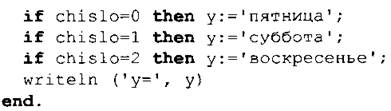
№ 15. Сумма координат соседних (т. e. имеющих общую сторону) полей на шахматной доске отличается на 1. Следовательно, если сумма координат некоторого поля является четным числом, то сумма координат всех его соседних полей будет нечетным числом и наоборот. Вместе с тем, соседние поля всегда имеют разный цвет.

№ 16

Задания в рабочей тетради

№ 180. При выполнении этого задания можно воспользоваться табл. 3.1 на с. 108 учебника.

№ 181. Правильно записаны условия 4, 7, 9 и 10. Во всех остальных случаях рекомендуется обсудить с учениками правильные варианты записи условий.

№ 183. Алгоритм поиска наименьшего (наибольшего) из трех чисел — один из ключевых алгоритмов, рассматриваемых в курсе информатики основной школы. Алгоритм поиска наибольшего из трех чисел рассматривался в примере 9 на с. 79 учебника. Важно, чтобы ученики могли увидеть общее и отличия в этих двух алгоритмах.

а	b	с	min
10	5	1	1
10	5	7	5
2	10	5	2

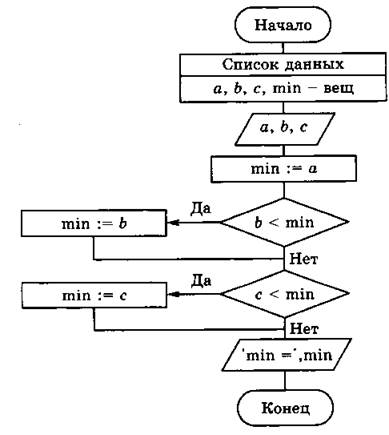
№ 184.

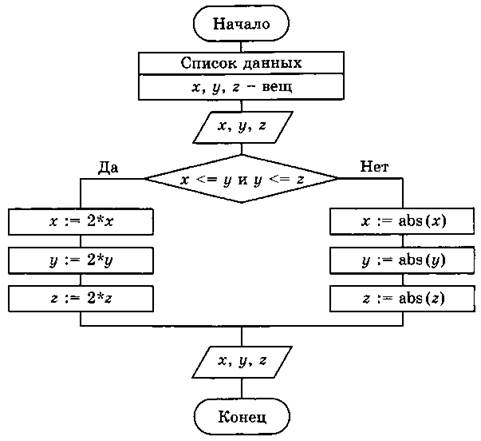
Ответ: если х ≤ у и у ≤ z, то исходные числа удваиваются, иначе определяются модули каждого числа.

№ 185. Ошибки: а) неправильно записано условие; не ставится знак “;” перед else и перед end; б) неправильно записано условие — простые условия следует взять в круглые скобки; не использован составной оператор после then и else.

Блок-схема:

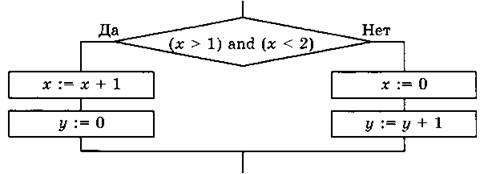
Правильный вариант записи фрагмента программы:

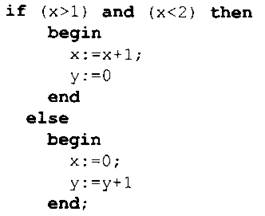
№ 186. При записи вложенных ветвлений надо помнить, что else всегда относится к ближайшему if.

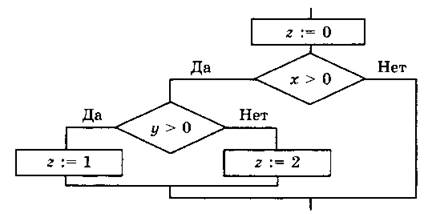
x	y	z
1	1	1
1	-1	2
-1	1	0
-1	-1	0

№ 187. Перед написанием программы рекомендуется перейти от графика функции к его аналитическому описанию: