закрепить изученный материал в ходе выполнения упражнений; рассмотреть различные случаи применения основных свойств корней n-й степени - КОРЕНЬ n-ОЙ СТЕПЕНИ И ЕГО СВОЙСТВА - ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ - 1-е полугодие

УРОК № 2

Урок типовых задач

Цели: закрепить изученный материал в ходе выполнения упражнений; рассмотреть различные случаи применения основных свойств корней n-й степени.

Ход урока

I. Устная работа

1. Дайте определение корня n-й степени из действительного числа.

2. Сколько значений имеет корень , если:

3. Какой корень называется арифметическим? Верно ли, что

4. Сформулируйте основные свойства корней.

5. Вынесите множители за знак корня (х > 0; у > 0):

6. Внесите множитель под знак корня (х > 0; у > 0):

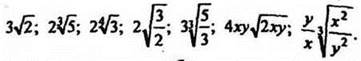
7. Представьте в виде число (х > 0, у > 0):

II. Самостоятельная работа бригадным методом (10-12 мин)

Учащиеся рассаживаются по группам по 4 человека (в каждой группе есть хорошо успевающий ученик) и выполняют самостоятельно № 399, 400, 401, 402, 403 из учебника.

III. Решение учителем типовых задач

1. Уничтожение иррациональности в знаменателе дроби.

Рассмотрим некоторые типичные случаи:

2. Применение тождеств сокращенного умножения к действиям с арифметическими корнями:

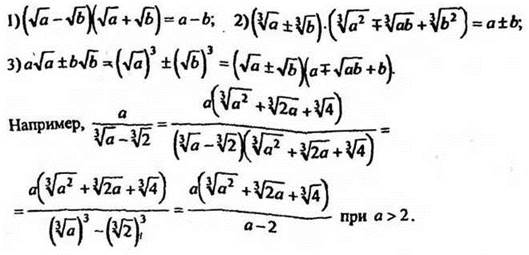
3*. Представить выражение в виде дроби, знаменатель которой не содержит радикала:

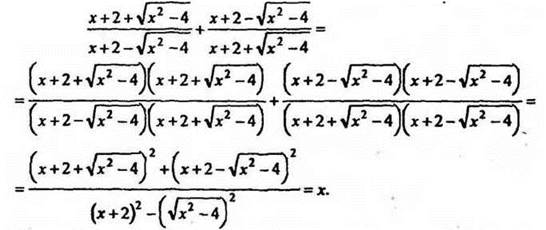
Каждая дробь имеет смысл, если знаменатель каждой дроби отличен от нуля и х2 - 4 ≥ 0.

4. Решить № 410 (в; г).

Решение

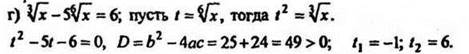
Если t = -1, то уравнение не имеет решений.

Если t = 6, то

Ответ: 66.

5. Решить № 415 (в; г) - самостоятельно, с последующей проверкой.

IV. Итоги урока

V. Домашнее задание: п. 32, решить № 398, № 406, № 407, № 408, № 409, № 410 (а; б), № 415 (а; б).