ввести понятие иррациональных уравнений и показать способы их решения - ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ - ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ - 1-е полугодие

УРОК № 1

Урок–лекция

Цели: ввести понятие иррациональных уравнений и показать способы их решения.

Ход урока

I. Итоги проверочной работы

1. Разобрать ошибки учащихся в работе.

2. Решить задание 6*:

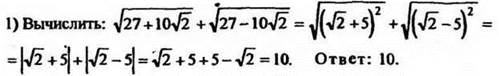
Подкоренные выражения не являются полными квадратами, т. е. применить приём из предыдущего примера не удаётся. Возведём вычисляемое выражение в квадрат:

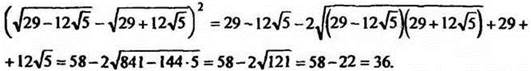
Следовательно, исходное выражение может быть равно 6 или -6; так как то это выражение отрицательно. Ответ: -6.

II. Объяснение нового материала (лекция)

1. Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.

2. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путём возведения в степень обеих частей уравнения или замены переменной.

3. При возведении обеих частей уравнения в чётную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.

4. Иногда удобнее решать иррациональные уравнения, определив область допустимых значений неизвестного и используя равносильные переходы.

5. Решим уравнения:

Решение

Возведём обе части уравнения в квадрат:

Проверка: 1) х = -1, тогда ложно;

2) х =2, тогда верно. Ответ: х = 2;

Решение

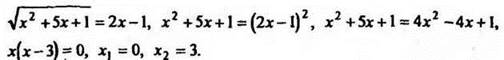
Проверка:

значит, х1 = 0 не удовлетворяет уравнению.

2) х2 = 3, тогда Значит, х = 3 – корень уравнения. Ответ: 3;

Решение

Возведя обе части уравнения в квадрат, получим 2х - 3 = х - 2, х = 1.

Проверка: Обе части уравнения не имеют смысла. Ответ: нет корней;

г) решить уравнение

Решение

Поскольку корни арифметические, то левая часть уравнения неотрицательна, а правая отрицательна, значит, уравнение решений не имеет. Ответ: уравнение решений не имеет;

д) решить уравнение

Решение .

Область допустимых значений неизвестного (ОДЗ) этого уравнения определяется системой неравенств 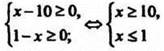которая решений не имеет. Уравнение не определено в множестве действительных чисел. Ответ: уравнение решений не имеет;

е) решить уравнение

Решение

По определению квадратного корня уравнение равносильно системе

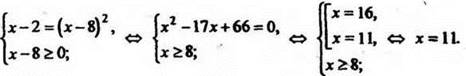
Ответ: 11.

III. Закрепление изученного материала

1. Решить № 417 (a).

2. Решить № 418 (а; б).

3. Решить №419 (а; г),.

Учащиеся решают самостоятельно, а затем проверяют своё решение с решением сильного ученика на переносной доске (сначала они не видят, как он решает).

IV. Итоги урока

V. Домашнее задание: п. 33 (до примера 6); решить № 417 (в), № 418 (в; г), № 419 (б; в), № 422 (а; г).