познакомить учащихся с решениями некоторых типов иррациональных уравнений; способствовать развитию навыка решения иррациональных уравнений - ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ - ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ - 1-е полугодие

УРОК № 2

Урок типовых задач

Цепи: познакомить учащихся с решениями некоторых типов иррациональных уравнений; способствовать развитию навыка решения иррациональных уравнений.

Ход урока

I. Устная работа .

1. Какие из следующих уравнений являются иррациональными:

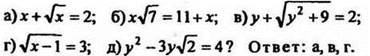
2. Является ли число х0 корнем уравнения:

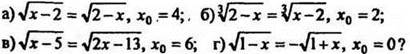
3. Найти область определения функции:

II. Решение иррациональных уравнений

Рассмотрим решение некоторых типов иррациональных уравнений.

1. Уравнения, в которых одно или несколько подкоренных выражений точные квадраты.

Решить уравнение

Решение

Приведём его к виду

а) если х < -2, то –х – 2 – х + 5 = 10, х = -3,5;

б) если -2 < х < 5, то х + 2 - х + 5 = 10, 7 = 10. Однако, 7 ≠ 10, следовательно, решений нет;

в) если х > 5, то х + 2 + х - 5 = 10, х = 6,5.

Ответ: х = -3,5 и х = 6,5.

2. Уравнения, содержащие несколько квадратных радикалов.

Пример I. Решить уравнение

Решение

Возведём обе части уравнения в квадрат, получим:

откуда найдём

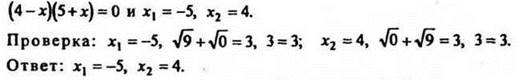
Пример 2. Решить уравнение

Решение

Допустимые значения неизвестного удовлетворяют условиям

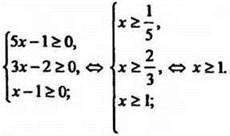
Уединяя один из радикалов и возводя обе части уравнения в квадрат, получаем:

Снова возводим обе части в квадрат:

Число х1 = 2/11 не принадлежит области определения данного уравнения, поэтому не может быть его корнем. Число х2 = 2 принадлежит ОДЗ, проверкой убеждаемся, что х = 2 является корнем уравнения. Ответ: х = 2.

3. Уравнения, содержащие корни третьей степени.

Пример 1. Решить уравнение

Указание. Решение примера 6 на стр. 208 учебника.

Пример 2. Решить уравнение

Решение

Воспользуемся формулой куба разности двух чисел

Возведя обе части данного уравнения в куб, получим уравнение равносильное данному. Допустим, что данное уравнение имеет решение, заменим второй множитель на 1, получим уравнение

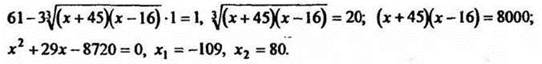
Проверкой убеждаемся, что это корни уравнения.

Ответ: х1 = -109; х2 = 80.

4. Иррациональные уравнения, решаемые способом замены.

Пример 1. Решить уравнение

Решение

Обозначим Получим то х = 1 или не имеет корней, т. к.

Пример 2. Решить уравнение

Решение

Введём новую переменную у = x2 + х. Тогда получим уравнение область определения которого задаётся условиями

Возведя обе части этого уравнения в квадрат, имеем:

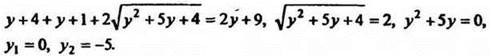
Значение y = -5 не входит в область определения уравнения. Значит,

Пример 3*. Решить уравнение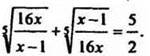

Решение

ОДЗ: х ≠ 1, х ≠ 0. Обозначим 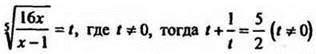или

Тогда: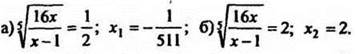

Ответ:

III. Итоги урока

IV. Домашнее задание: п. 33; решить № 420, 423 (а; б), № 424 (а; б), № 425 (а; б).