использовать свойства показательной функции для решения показательных уравнений, показать способы их решения - РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие

Цели: использовать свойства показательной функции для решения показательных уравнений, показать способы их решения.

Ход урока

I. Объяснение нового материала

1. Повторить основные свойства показательной функции.

2. Уравнение, содержащее переменную в показателе степени, называется показательным.

Простейшим примером показательного уравнения служит уравнение Это уравнение можно решать графически.

Область значений функции у = ах - множество положительных чисел. Поэтому в случае b < 0 или b = 0 уравнение аx = b не имеет решений.

Если b > 0, то уравнение аx = b(а > 0, а ≠ 1) имеет единственный корень.

3. Решение показательного уравнения вида основано на том, что это уравнение равносильно уравнению f(х) = g(x).

4. Рассмотреть решение уравнений в примерах 1, 2, 3 и 4 на стр. 221 учебника и записать их решение в тетрадях.

II. Закрепление изученного материала

1. Решить уравнения: с № 460 по № 464 включительно (решаем задания в и г).

2. Решить уравнение

Решение

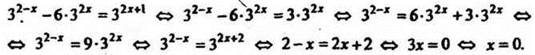
Ответ: 0.

3. Решить уравнение

Решение

Представим данное уравнение в виде

Обозначим Поэтому

Ответ: х1 = -2, х2 = 2.

III. Итоги урока

IV. Домашнее задание: п. 36(1); решить с № 460 (а; б) по №а 464 (а; б) включительно; решить № 163 на стр. 286.