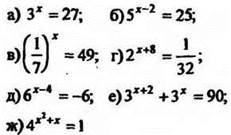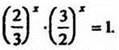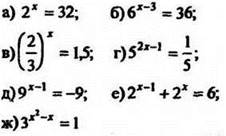показать другие приёмы решения показательных уравнений; рассмотреть решение систем уравнений показательных - РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие

Цели: показать другие приёмы решения показательных уравнений; рассмотреть решение систем уравнений показательных.

Ход урока

I. Математический диктант (5 -8 мин)

Вариант I	Вариант II
1. Решить уравнения: 2*. Решите уравнение Ответ: R, т. е. любое действительное число.	1. Решить уравнения: 2*. Решите уравнение Ответ: нет решений.

II. Решение показательных уравнени.

1. Решить уравнения (объясняет учитель):

Решение

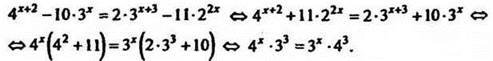
Так как 3x ≠ 0 и 33 ≠ 0, то, разделив обе части уравнения на 3x · 33 > 0, получим откуда x = 3. Ответ: х = 3;

Разделив обе части уравнения на 8x > 0, получим Обозначим отсюда

t - 1 = 0 или t2 + t + 2 = 0,

t = 1 или D = 1 - 8 = -7 < 0 нет решений.

Если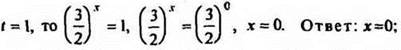

Решение

Разделив обе части уравнения на 36х ≠ 0, получим:

Положим тогда имеем (при у ≠ 0):

Значит,

2. При решении, показательных уравнений часто пользуются искусственными приёмами:

а) решить уравнение

Решение

Воспользуемся тем, что 5х > 0 при любом х, и перейдём к равносильному уравнении:

Заметим, что х = 2 - решение этого уравнения. Покажем, что других решений нет. Функция как сумма двух убывающих функций является убывающей, а потому каждое своё значение она принимает только один раз. Ответ: х = 2;

б) решим уравнение

Решение

Заметив, что вводим новую переменную Полученное после этого уравнение имеет два корня которым соответствуют два решения данного уравнения х1 = -2, х2 = 2. Ответ: -2;2.

III. Решение систем показательных уравнений

1. Рассмотреть решение примера 8 на стр. 222.

2. Решить № 465 (г) - на доске и в тетрадях.

Решение

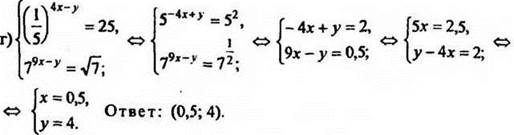
3. Самостоятельно решить № 465 (в) и № 470 (а; б).

IV. Итоги урока

V. Домашнее задание: п. 36; решить № 468-470 (в; г) и № 465 (а; б).