Алгебра и начала анализа для учащихся 11 класса поурочные планы
ввести определение логарифмической функции и рассмотреть её свойства - ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие
Цели: ввести определение логарифмической функции и рассмотреть её свойства.
Ход урока
I. Выполнение упражнений для закрепления изученного материала.
1. Устно:
а) какие из выражений имеют смысл:
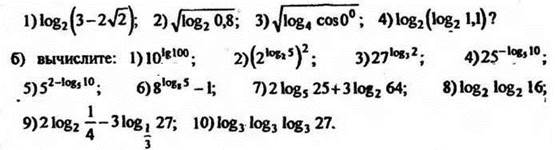
2. Записать в тетрадях:
1) логарифм степени равен произведению показателя степени на логарифм её основания, то ест.
![]()
если N < 0, а с - чётное число, то справедлива формула
![]()
Например, ![]()
2) если основание логарифма и число, стоящее под знаком логарифма, возвести в одну и ту же степень, отличную от нуля, то значение логарифма не изменится, то есть
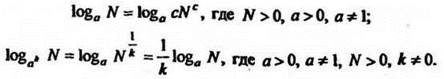
Например, ![]()
3) упростить 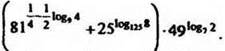
Решение
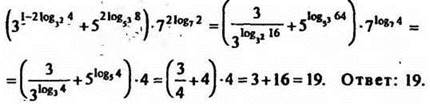
II. Изучение нового материала
1. Определение логарифмической функции.
2. Основные свойства логарифмической функции.
3. График логарифмической функции (рис. 135).
4. Симметричность графиков логарифмической и показательной функций, имеющих одинаковое основание, относительно прямой у = х (рис. 136).
5. Рассмотреть по учебнику примеры применения свойств логарифмической функции: на стр. 230-231 примеры 1, 2, 3, 4 и 5.
III. Закрепление изученного материала
1. Найти область определения функции.
![]()
Решение
D(у) = R+, поэтому заданная функция определена только для тех х, при которых 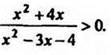
Решая методом интервалов неравенство 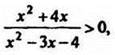 находим, что
находим, что 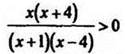

Рис. 23
![]()
2) самостоятельно решить № 500 (б; г).
2. Сравните числа: решить № 501 (устно) и № 503 (б; г).
IV. Итоги урока
V. Домашнее задание: п. 37 и а 38; самостоятельно изучить п. 40; решить № 499, № 500 (а; в), № 503 (а; в), № 510 и № 506. Подготовиться к письменному зачёту по теме «Логарифмы и их свойства. Логарифмическая функция)».