Производная. Применения непрерывности и производной - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие

УРОК № 4

Тема. Производная. Применения непрерывности и производной

Цели: повторить правила вычисления производных и производные функций; закрепить навыки решения неравенств и составления уравнений касательных к графику функции.

Ход урока

I. Итоги домашней работы

Учащиеся писали домашнюю работу на листочках. Учитель сообщает, как усвоен материал решения тригонометрических уравнений и неравенств.

II. Повторение изученного материала

1. Понятие производной.

2. Правила вычисления производных.

3. Производная сложной функции.

4. Производные тригонометрических функций.

5. Применения непрерывности.

6. Касательная к графику функции.

7. Производная показательной и логарифмической функций.

III. Решение задач

1. Найдите значение производной функции

Решение

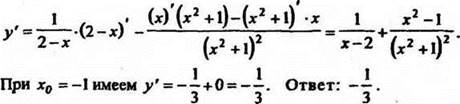
2. Решить неравенство:

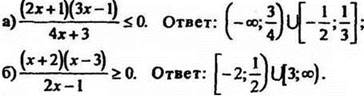
3. Вычислить значение производной функции

Указание. Ответ:

4. Найдите область определения каждой из функций:

Решение

Функция у = определена, если значение подкоренного выражения неотрицательно.

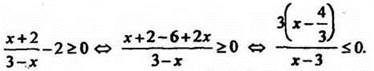
При условии х ≠ 3 решим неравенство методом интервалов:

Рис. 49

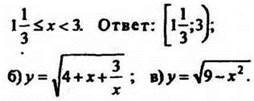
5. Найдите наименьшие целые решения неравенства хб + 9х3 + 8 ≤ 0.

Решение

Обозначим х3 = у, тогда

Рис. 50

Наименьшее целое решение х = -2. Ответ: -2

6. Найти область определения функции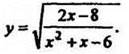

Ответ: (-3;2)U[4;∞).

7. Составить уравнение касательной к графику функции в точке его пересечения с осью ординат.

Решение

Уравнение касательной

Точка пересечения с осью OY:

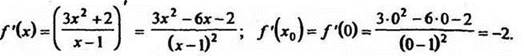
Искомое уравнение карательной имеет вид у = -2 - 2(х - 0) = -2х - 2.

Ответ: у = -2х - 2.

8. Напишите уравнение касательной к графику функции в точке с абсциссой х0 = -0,5.

Решение

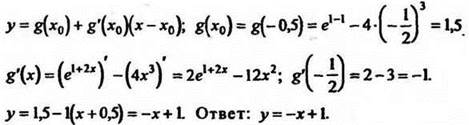
9. Самостоятельно: напишите уравнение касательной к графику функции в точке х0 = 3. Ответ: у = 3х - 9.

10. В интервале [;2) найти абсциссу точки, в которой касательная к кривой у = cos х + 2х + 4 параллельна прямой у = 2х + 10.

Решение

Прямые параллельны, если k1 = k2, a b1 ≠ b2. Составим уравнение касательной к кривой у = cosx + 2х + 4; найдем производную

Угловой коэффициент касательной равен f'(х0). Значит, k = f'(х0).

Т.к. f'(x0) = k, тогда

Интервалу [;2) принадлежит точка х0 = . Ответ: .

11. Самостоятельно: в интервале [0;] найти абсциссу точки, в которой касательная к кривой у = sin2х + 3х + 1 параллельна прямой у = 3x + 4.

Ответ: /4.

IV. Итоги урока

V. Домашнее задание: повторить из § 6, п. 22, 23, 24; решить на стр. 167 № 4 (3) и № 5; на стр. 292 № 219-221.