Применение производной к исследованию функции - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие

УРОК № 5

Тема. Применение производной к исследованию функции

Цели: повторить признак возрастания (убывания) функции, нахождение критических точек функции, её максимумов и минимумов; рассмотреть примеры применения производной к исследованию функции.

Ход урока

I. Устная работа

1. Сформулировать признак возрастания (убывания) функции.

2. Определение критических точек функции.

3. Сформулируйте признак максимума (минимума) функции.

4. Опишите схему исследования функции.

II. Выполнение упражнений

1. Найти промежутки монотонности функции

Решение

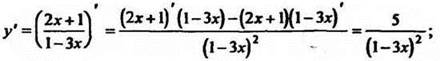
при х - любое действительное число, кроме x = 1/3.

Т. к. у’ > 0 на промежутке то функция на этом промежутке возрастает.

Ответ: функция возрастает на

2. Самостоятельно: найти промежутки монотонности функции

Ответ: убывает на

3. Найдите критические точки функции и укажите среди них одну из точек максимума.

Решение

Рассмотрим функцию на промежутке (0;2). При х = /3 у' > 0; при х = у' <0.

Таким образом, х = /2 -точка максимума.

Ответ: критические точки: одна из точек максимума /2.

4*. При каких значениях а график функции у = 3х – 4x3 и прямая у= а имеют одну общую точку?

Решение

Найдем /фонзводную найдём те значения х, при которых производная равна нулю:

Определим промежутки знакопостоянства производной:

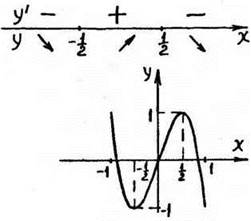
Рис. 52

На интервале функция y(х) убывает и принимает значения, заполняющие промежуток [-1;∞).

На отрезке функция возрастает и принимает значения [-1;1].

На функция убывает и принимает значения (-∞;1].

Таким образом, прямая у = а имеет с графиком данной функции одну общую точку при а < -1 или а > 1.

Ответ: при а < -1 или а > 1.

5. Исследуйте функцию на возрастание и убывание на отрезке и найдите экстремумы функции на этом отрезке.

Решение

Найдем критические точки функции из условия f'(х) = 0:

cos x = 0 или sin x = 0,5.

или

На заданный в условии отрезок попадают точки

Эти точки разбивают данный промежуток на три промежутка:

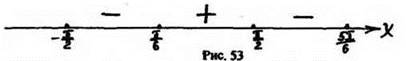
Определим знак производной в произвольной точке каждого промежутка:

Ответ: функция убывает на и на 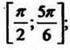функция возрастает на 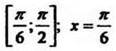является точкой минимума, х = /2 есть точка максимума.

6. Исследовать функцию и построить её график.

III. Итоги урока

IV. Домашнее задание: повторить из § 6 п. 25 «Наибольшее и наименьшее значения функции»; решить на стр. 294 № 230 (а; б); № 231 (б; г); № 232 (б; в).