Алгебра и начала анализа для учащихся 11 класса поурочные планы
Показательная функция. Решение показательных уравнений и неравенств - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие
УРОК № 10
Тема. Показательная функция. Решение показательных уравнений и неравенств
Цели: способствовать выработке навыка решения показательных уравнений и неравенств.
Ход урока
I. Итоги самостоятельной работы
II. Повторение изученного материала
1. Дайте определение показательной функции.
2. Перечислите основные свойства показательной функции.
3. Изобразите схематически график функций:
![]()
4. Как используются свойства показательной функции при решении показательных уравнений и неравенств?
III. Выполнение упражнений
1. Решить уравнение ![]()
Решение
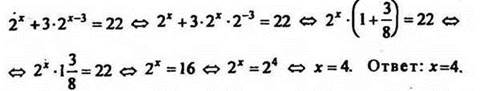
2. Решить уравнение ![]()
Решение
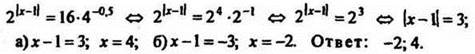
3. Решить уравнение ![]()
Решение
ОДЗ x ≥ 0. Замена ![]() где y > 0 приводит к уравнению
где y > 0 приводит к уравнению ![]() имеющему корни у = -1 и у = 2. Уравнение
имеющему корни у = -1 и у = 2. Уравнение ![]() имеет решение х = 1, а уравнение
имеет решение х = 1, а уравнение ![]() решений не имеет, т, к.
решений не имеет, т, к. ![]() для всех значений х ≥ 0. Ответ: х = 1.
для всех значений х ≥ 0. Ответ: х = 1.
4. Решить уравнение ![]()
Указание. После деления обеих частей уравнения на 4х (4х ≠ 0 при всех значениях х) получим равносильное уравнение, которое после замены 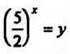 приводится к квадратному уравнению
приводится к квадратному уравнению ![]()
Ответ: ![]()
5. Самостоятельно решить уравнение ![]()
Указание. Разделим обе части на ![]() получим
получим ![]() замена
замена ![]() даёт уравнение
даёт уравнение ![]() Ответ: х = 1/2,
Ответ: х = 1/2,
6. Решить уравнение ![]()
Указание. ![]() Обозначим
Обозначим ![]() где y > 0 и решим уравнение
где y > 0 и решим уравнение ![]() Ответ: х = 2.
Ответ: х = 2.
7. Решить уравнение ![]()
Решение
![]()
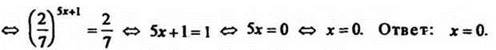
8*. Решите уравнение ![]()
Решение
Заметим, что ![]() Сделав замену
Сделав замену ![]() получим уравнение
получим уравнение ![]() решениями которого являются числа
решениями которого являются числа ![]() Значит,
Значит, ![]() или
или ![]() . Решениями этих уравнений являются соответствующие числа 2 и -2, т. к.
. Решениями этих уравнений являются соответствующие числа 2 и -2, т. к. ![]()
Ответ: х = 2, х = -2.
9. Решите неравенство ![]()
Решение
![]() Обозначим 2х = у, где y > 0 и решим неравенство
Обозначим 2х = у, где y > 0 и решим неравенство ![]() методом интервалов:
методом интервалов: ![]()

![]()
10. Решите неравенство ![]()
Решение
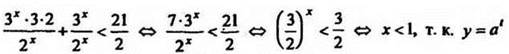 возрастающая функция при а > 1. Ответ: (-∞;1).
возрастающая функция при а > 1. Ответ: (-∞;1).
11. Решите неравенство ![]()
Указание. Поделить обе части неравенства на 32х и сделать замену ![]() где y > 0. Ответ: (-∞;-2).
где y > 0. Ответ: (-∞;-2).
12. Решите неравенство 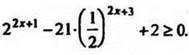
Решение
Сделав замену у = 22х+1, приходим к системе неравенств
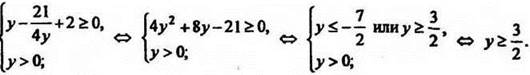
Переходим к переменной х: ![]() Т. к. у = 2 -возрастающая функция, то
Т. к. у = 2 -возрастающая функция, то ![]() Ответ:
Ответ: ![]()
13. Самостоятельно решить неравенства:
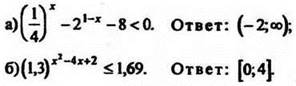
IV. Итоги урока
V. Домашнее задание: повторить из § 10 п. 37 -39; из § 11 п. 41, 42; решить на стр. 286 № 164-166, № 168, № 169.