Графический способ решения уравнений - ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цель: использование графиков функций для решения или исследования уравнений.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Катер прошел 46 км по течению реки и 17 км против течения, затратив на весь путь 3 ч. Найти собственную скорость катера, если скорость течения реки 3 км/ч.

2. Знаменатель несократимой обыкновенной дроби на 7 больше ее числителя. Если числитель дроби увеличить на 3, а ее знаменатель уменьшить на 3, то полученная дробь будет на 11/18 больше данной дроби. Найдите данную дробь.

Вариант 2

1. Катер прошел 20 км по течению реки и 32 км против течения, затратив на весь путь 3 ч. Найти собственную скорость катера, если скорость течения реки 2 км/ч.

2. Знаменатель несократимой обыкновенной дроби на 5 больше ее числителя. Если числитель дроби увеличить на 2, а ее знаменатель уменьшить на 2, то полученная дробь будет на 18/35 больше данной дроби. Найдите данную дробь.

III. Изучение нового материала (основные понятия)

Во многих случаях для решения или исследования уравнений используют графики функций.

Пример 1

Решим уравнение х2 + 2 = 3/x.

В одной координатной плоскости построим графики функций у1 = х2 + 2 и у2 = 3/x. Видно, что эти графики пересекаются в единственной точке А (1; 3). Абсцисса точки пересечения А есть то значение переменной х, при котором значения функций у1 и у2 равны (или выражения х2 + 2 и 3/x принимают равные значения). Итак, данное уравнение х2 + 2 = 3/x имеет единственный корень х = 1.

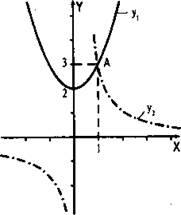
Заметим, что для нахождения корня данного уравнения могут быть рассмотрены графики и других функций. Учтем, что в уравнении х2 + 2 = 3/x величина х ≠ 0. Умножим все члены уравнения на х и получим равносильное уравнение: х3 + 2х = 3 или х3 = 3 - 2х. Построим графики функций у1 = х3 и у2 = 3 - 2х. Видно, что графики этих функций пересекаются в единственной точке А (1; 1). При х = 1 значения функций у1 и у2 равны (или выражения х3 и 3 - 2х принимают равные значения). Итак, х = 1 — единственный корень данного уравнения.

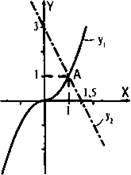
Рассмотренный способ решения уравнения называют графическим.

Пример 2

Графически решим уравнение х2 = |х - 1|.

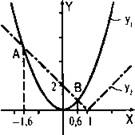
В одной системе координат построим графики функций у1 = х2 и у2 = |х - 1|. Видно, что эти графики пересекаются в двух точках А и В. Приближенное значение абсцисс этих точек х1 ≈ -1,6 и х2 ≈ 0,6 соответственно. Заметим, что решив аналитически данное уравнение, получим

Пример 3

При различных значениях параметра а определите число корней уравнения х2 - |х| + а = 0.

Данное уравнение запишем в виде х2 + a = |х|. Построим график функций у1 = х2 + а и у2 = |х|. График функции у2 не зависит от параметра а. График функции у1 представляет собой параболу, вершина которой имеет координаты (0; а). С уменьшением параметра а парабола смещается вниз.

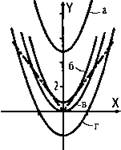
При достаточно больших значениях а графики у1 и у2 не имеют общих точек (случай а). Уравнение при этом решений не имеет. При уменьшении параметра а парабола спускается вниз и касается зависимости у2 в двух точках (случай б). Тогда уравнение имеет два корня. При дальнейшем уменьшении а парабола пересекает каждую ветвь графика у2 в двух точках (этот случай на рисунке не изображен). При этом уравнение имеет четыре корня. При а = 0 парабола расположена еще ниже и пересекает графику в трех точках (случай в). Тогда уравнение имеет три корня. При дальнейшем уменьшении а (т. е. при а < 0) парабола пересекает график у2 в двух точках (случай г) и уравнение имеет два корня.

Определим, при каком значении параметра а реализуется случай б. Так как графики функций у1 и у2 симметричны относительно оси ординат, то достаточно рассмотреть случай x ≥ 0. Для таких значений х по определению |х| = х и данное уравнение имеет вид х2 - х + а = 0. Так как в рассматриваемом случае в области х ≥ 0 уравнение имеет один корень, то дискриминант уравнения D = 1 - 4а - 0, откуда а = 1/4.

Итак, опишем полученные результаты (в порядке возрастания параметра а): при а < 0 или а = 1/4 - 2 корня, при a = 0 - 3 корня, при 0 < а < 1/4 – 4 корня, при а > 1/4 - нет корней.

IV. Задание на уроке

№ 622 (а); 624; 626; 627 (а); 628 (а).

V. Задание на дом

№ 622 (б); 623; 625; 627 (б); 629 (б); 629.

VI. Творческие задания

1. Графически решите уравнение;

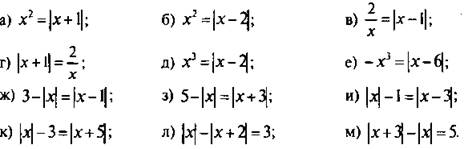
Ответы:

а) х1 = -0,6 и х2 = 1,6.

б) х1 = -2 и х2 = 1; .

в) х = 2;

г) х = 1; .

д) х = 1; .

е) х = -2;

ж) х1 = -1 и х2 = 2;

з) х1 = -4 и х2 = 1; .

и) х = 2;

к) х = -4; .

л, м) корней нет.

2. Определите число корней уравнения:

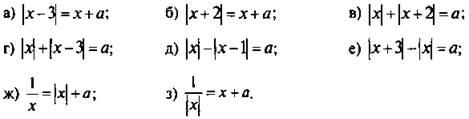
Ответы:

а) при а < -3 — корней нет, при а = -3 — бесконечно много корней, при а > -3 — 1 корень;

б) при а < 2 — корней нет, при а = 2 — бесконечно много корней, при а > 2 — 1 корень;

в) при а < 2 — корней нет, при а = 2 — бесконечно много корней, при а > 2 — 2 корня;

г) при а < 3 — корней нет, при а = 3 — бесконечно много корней, при а > 3 — 2 корня;

д) при а < -1 или а > 1 — корней нет, при а = -1 или а = 1 — бесконечно много корней, при -1 < а < -1 — 1 корень;

е) при а < -3 или а > 3 — корней нет, при а = -3 или а = 3 — бесконечно много корней, при -3 < а < -3 — 1 корень;

ж) при а< -2 — 3 корня, при а = -2 — 2 корня; при а > -2 — 1 корень;

з) при а < 2 — 1 корень, при а = 2 — 2 корня, при а > 2 — 3 корня.

VII. Подведение итогов урока