Деление дробей - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: изучить деление дробей.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (тест).

Вариант 1

1. Выполните умножение

Ответы:

2. Умножьте дроби

Ответы:

3. Упростите выражение

Ответы:

Вариант 2

1. Выполните умножение

Ответы:

2. Умножьте дроби

Ответы:

3. Упростите выражение

Ответы:

III. Изучение нового материала (основные понятия)

При делении обыкновенных дробей операцию деления заменяют операцией умножения. При этом первую дробь умножают на дробь, обратную второй. Например Таким же образом можно делить и рациональные дроби, т. е. Докажем это равенство для любых допустимых значений переменных, т. е. для b ≠ 0, c ≠ 0 и d ≠ 0. Для этого надо доказать, что произведение выражения и дроби c/d равно дроби a/b. Проверим это. Получаем: Из равенства по определению частного имеем:

Из полученного тождества следует правило деления дробей: чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

Используя правило деления дробей и правило умножения дробей, получим:

Пример 1

Разделим дробь на дробь

Используя правило деления дробей, получим: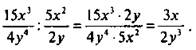

Пример 2

Разделим дробь на дробь

Воспользуемся правилом деления дробей. Имеем:

Пример 3

Разделим многочлен а – 2b на дробь

При делении многочлена на дробь (или наоборот), как и ранее, записывают многочлен в виде дроби со знаменателем 1 и используют правило деления дробей. Имеем: (a - 2b):

Заметим, что на двух последних занятиях были использованы свойства степеней. Поэтому напомним эти свойства:

1. (при умножении степеней с одинаковыми основаниями показатели степеней складываются, а основание остается прежним).

2. (при делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остается прежним).

3. (при возведении степени в степень показатели степеней умножаются, а основание остается прежним).

4. (при возведении в степень произведения чисел в эту степень возводится каждый множитель и результаты перемножаются).

5. (при возведении в степень дроби в эту степень возводится числитель и знаменатель дроби и результаты делятся).

IV. Контрольные вопросы

1. Как делятся рациональные дроби?

2. Докажите правило деления дробей.

V. Задание на уроке

№ 131 (а, д); 132 (а, в); 134 (а, б); 136 (а, в, д); 138 (а, б, д); 139 (a); 140 (а, в); 141 (а).

VI. Задание на дом

№ 131 (б, е); 132 (б, г); 133 (г); 134 (в, г); 135 (а, г); 136 (б, г, е); 137 (г, е); 139 (б); 140 (б, г); 141 (в).

VII. Подведение итогов урока