Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Алгебраические уравнения и системы
Ответы к упражнениям на с. 42, 43 и 52.
1. Абсолютное тождество, так как верно при всех без исключения значениях x.
2. Абсолютное тождество. Верно при x ≠ π/2 + kπ. Если же x = π/2 + kπ, то обе части теряют смысл.
3. Неабсолютное тождество. Область определения левой части: x ≠ π/2 + kπ, область определения правой части: x ≠ kπ/2.
4—6. Тождество 4 является абсолютным, поскольку это определение секанса. Тождества 5 и 6 неабсолютные, так как правые части определены всегда, в то время как левые могут терять смысл.
7—8. Тождество 7 абсолютное. B самом деле, левая часть теряет смысл при cos x/2 = 0. Правая часть может быть записана в виде
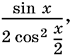
т. е. тоже теряет смысл при cos x/2 = 0.
Тождество 8 неабсолютное. Левая часть теряет смысл при cos x/2 = 0, а правая, которая может быть записана в виде
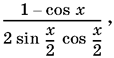
перестает существовать как при cos x/2 = 0, так и при sin x/2 = 0.
9—10. Левую часть равенства 9 можно преобразовать так:
ctg 2x = cos 2x/sin 2x = cos 2x/2sin x cos x,
а правую записать в виде
![]()
Обе части этого равенства перестают существовать одновременно, если либо cos x = 0, либо sin x = 0, следовательно, тождество 9 абсолютное.
Тождество 10 является неабсолютным, поскольку при x = π/2(2n + 1) левая часть равна нулю, а правая теряет смысл.
11—13. Первое из этих трех тождеств неабсолютное, второе и третье — абсолютные.
14—16. Первое и второе тождества неабсолютные, третье — абсолютное.
B самом деле, для первого область определения левой части: x > 0, y > 0; x < 0, y < 0, а область определения правой части: x ≠ 0; y ≠ 0. Для второго область определения левой части x ≠ 0, а область определения правой части x > 0.
Наконец, для третьего x ≠ 0 для обеих частей тождества.
17. Пусть x = а — корень данного уравнения. Тогда f(а) = φ(а). Поскольку ψ(x) существует при всех x, то ψ(а) — число; следовательно,
f(a) + ψ(а) = φ(а) + ψ(а). (1)
Таким образом, x = а — корень уравнения
f(x) + ψ(x) = φ(x) + ψ(x). (2)
Обратно: если x = а — корень (2), то имеет место равенство (1), а потому x = а — корень уравнения f(x) = φ(x).
Вторую часть теоремы доказывает пример. B самом деле, достаточно рассмотреть два уравнения:
x − 1 = 0 и x − 1 + 1/x − 1 = 1/x − 1,
первое из которых имеет единственный корень x = 1, а второе вовсе не имеет корней, так как при x = 1 оно теряет смысл.
18. Доказательство аналогично 17. Даже пример можно взять тот же самый.
19—19а. Для доказательства достаточно заметить, что посторонними для данного уравнения могут быть те корни уравнения
f(x) = ψ(x),
для которых φ(x) либо не существует, либо обращается в нуль.
20. Если f(а) = φ(а), то [f(а)]² = [φ(а)]². Обратно: из второго равенства следует, что либо f(а) = φ(а), либо f(а) = −φ(а).
21. Система равносильна совокупности четырех систем:

22. Доказательство непосредственно следует из свойств пропорций.
9.1. При x < −2 получим
−x + 2x + 2 − 3x − 6 = 0,
т. е. x = −2, что противоречит предположению. Таким образом, при x < −2 уравнение не имеет решений.
При −2 ≤ x ≤ −1 получим x = −2.
При −1 < x ≤ 0 уравнение обращается в ложное числовое равенство 4 = 0. На этом интервале нет решений.
Наконец, при x > 0 получаем x = −2, что снова противоречит ограничению.
Ответ. x = −2.
9.2. Пусть x² = y. Тогда
|y − 9| + |y − 4| = 5.
Точки y = 4 и y = 9 разбивают числовую ось на три интервала.
Если y < 4, уравнение примет вид
9 − y + 4 − y = 5,
откуда y = 4. Это значение не принадлежит выбранному интервалу.
Если 4 ≤ y ≤ 9, то знаки абсолютной величины следует раскрыть так:
9 − y + y − 4 = 5, т. е. 5 = 5.
Так как уравнение обратилось в верное числовое равенство, то все значения y из интервала 4 ≤ y ≤ 8 являются решениями.
При y > 9 получим
y − 9 + y − 4 = 5,
т. е. y = 9. Здесь снова нет решений. Вспоминая, что y = x², запишем
4 ≤ x² ≤ 9, или 2 ≤ |x| ≤ 3.
Ответ. −3 ≤ x ≤ −2; 2 ≤ x ≤ 3.
9.3. Способ 1. Дополним стоящую слева сумму квадратов до полного квадрата:
(x − 3x/3 + x)² + 6x²/3 + x − 7 = 0,
т. е.
(x²/3 + x)² + 6x²/3 + x − 7 = 0,
откуда получаем совокупность уравнений:
x²/3 + x = −7, x²/3 + x = 1.
Действительных решений y этой совокупности уравнений нет.
Способ 2. Введем новое неизвестное:
3x/3 + x = u, или 3x = 3u + xu.
Получим систему
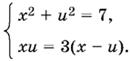
Вычитая из первого уравнения удвоенное второе, придем к уравнению относительно x − u
(x − u)² + 6(x − u) − 7 = 0, откуда следует совокупность двух уравнений:
x − u = −7, x − u = 1.
Решая каждое из этих уравнений, убедимся, что действительных корней нет.
Ответ. Решений нет.
9.4. Возведем данное уравнение в куб:
![]()
Стоящий в скобках в левой части уравнения двучлен заменим правой частью данного уравнения и приведем подобные члены:
![]()
Такая замена может привести к появлению посторонних корней. B самом деле, при возведении а + b = с в куб мы получаем равенство, справедливое при всех тех же значениях а, b и с, что и данное равенство. После замены же мы получим
а³ + b³ + 3аbс = с³.
Это равенство удовлетворяется при а = b = 1, с = −1, в то время как исходное равенство а + b = с при этих значениях букв ложно. Следовательно, мы должны завершить решение проверкой.
Возведем последнее иррациональное уравнение в куб. После сокращения получим
4х(2x − 3)(x − 1) = 9(x − 1)³.
Один корень этого уравнения x1 = 1; остается квадратное уравнение
x² − 6х + 9 = 0, x2,3 = 3.
Сделав проверку, убеждаемся, что найденные корни подходят.
Ответ. x1 = 1; x2,3 = 3.
9.5. Пусть
![]()
Придем к системе
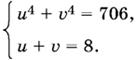
Это — симметрическая система, ее обычно решают подстановкой: и + V = в, ии = _. Поэтому преобразуем левую часть первого уравнения:
u4 + v4 = (u² + v²)² − 2u²v² = [(u + v)² − 2uv]² − 2u²v² = (64 − 2t)² − 2t² = 64² − 256t + 2t².
Поскольку все это равно 706, получаем квадратное уравнение
t² − 128t + 1695 = 0,
откуда
t1 = 15, t2 = 113.
Остается решить совокупность двух систем:
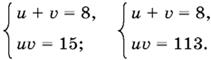
Решая первую, найдем v1 = 3, v2 = 5, откуда x1 = 4, x2 = 548. Вторая не имеет действительных решений.
Проверкой убеждаемся, что найденные корни удовлетворяют исходному уравнению.
Ответ. x1 = 4; x2 = 548.
9.6. Введем новые неизвестные:
![]()
Получим систему
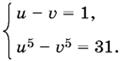
Обозначим u + v = p. Так как в силу первого уравнения системы u − v = 1, то u = p + 1/2, v = p − 1/2. Второе уравнение системы примет вид
(p + 1/2)5 − (p − 1/2)5 = 31,
или после очевидных упрощений
р4 + 2р² − 99 = 0.
Это биквадратное уравнение имеет два действительных корня р1 = −3, р2 = 3. Зная р1 и р2, найдем u1 = −1, u2 = 2, откуда получим два уравнения для определения значений x:
x² − 34x + 32 = 0, x² − 34x + 65 = 0.
Решив эти уравнения, найдем четыре корня.
Ответ.
![]()
9.7. Введем новые неизвестные:
![]()
т. е. u4 + v4 = а − b.
Получаем систему
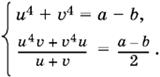
Заменяя во втором уравнении а − b на u4 + v4, получим
![]()
откуда
u5 + v5 − uv4 − и4v = 0, где u + v ≠ 0,
т. е.
u4(u − v) − v4(u − v) = 0,
а потому
(u − v)²(u² + v²)(u + v) = 0.
Так как последние два множителя в нуль обратиться не могут, то остается и = v, т. е. а − x = x − b, и, следовательно,
x = а + b/2.
Проверкой убеждаемся, что это — корень исходного уравнения, если а > b.
Ответ. При а > b имеем x = а + b/2.
9.8. Обозначив
![]()
получим систему уравнений
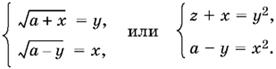
Вычитаем из первого уравнения второе:
x + y = (y − x)(x + y).
Если x + y = 0, то x = y = 0, поскольку и x, и y неотрицательны. Так как
![]()
то из x = y = 0 следует, что а = 0. Проверкой убеждаемся, что найден корень данного уравнения.
Если x + y ≠ 0, то y − x − 1 = 0, откуда
![]()
и x² + x + 1 − а = 0. Решая квадратное уравнение, найдем
![]()
Остается исследовать, при каких значениях а эти корни вещественны и удовлетворяют исходному уравнению.
Во-первых, необходимо, чтобы дискриминант был неотрицательным, т. е. а ≥ ¾ .
Во-вторых, корень данного уравнения не должен быть отрицательным. Один из корней
![]()
при всех а ≥ ¾ отрицателен, а потому не подходит. Другой корень
![]()
больше или равен нулю, если
![]()
т. е. а ≥ 1.
Проверкой убеждаемся, что
![]()
удовлетворяет первоначальному уравнению. B самом деле, подставляя x1 в это уравнение, получим
![]()
что выполняется одновременно с равенством
![]()
так как x ≥ 0. Значение х1 было найдено из уравнения
![]()
Поэтому можно осуществить в полученном нами равенстве соответствующую замену:
a − 1 − x1 = x1².
Так как в результате мы пришли к уравнению, из которого определили х1, то проверку можно считать законченной.
Ответ. x = 0, если а = 0, и
![]()
если а ≥ 1.
9.9. Перенесем
![]()
в правую часть уравнения:
![]()
и возведем обе части в квадрат. Получим
![]()
откуда при а ≠ 0
![]()
Делаем проверку, подставляя найденное значение x в данное уравнение. B левой части получим
![]()
Чтобы вычислить это выражение, нужно рассмотреть четыре различных случая, так как значения −1, 0, +1 параметра а разбивают числовую ось на четыре интервала. Однако легко заметить, что а > 0, так как разность, стоящая в левой части исходного уравнения, всегда положительна. Следовательно, остается рассмотреть только два случая.
Если 0 < а ≤ 1, то
![]()
Если же а > 1, то
![]()
Число 1/а равно числу а только при а = ±1, а по предположению а > 1.
Ответ.
![]()
если 0 < а ≤ 1.
9.10. Рассмотрим два случая.
Если 2x² − 3x − 2 ≥ 0, т. е. x ≤ −½, x ≥ 2, получим уравнение
4х² + 5х − 2(1 + β) = 0.
Корни этого уравнения
![]()
должны лежать вне интервала (−½, 2).
Неравенство
![]()
удовлетворяется при β ≥ −57/32. Больше двух этот корень быть не может.
Для x2 нужно решить два неравенства:
![]()
Первое выполняется при −57/32 ≤ β ≤ −7/4, а второе — при β ≥ 12.
Пусть теперь 2x² − 3x − 2 < 0, т. е. −½ < x < 2. Данное уравнение станет линейным и мы найдем
x3 = 2(β − 1)/11.
Решим неравенство
−½ < 2(β − 1)/11 < 2
и получим
−7/4 < β < 12.
Итак, при β = −57/32 корни х1 и х2 совпадают, а корень х3 не существует, т. е. уравнение имеет единственное решение x = −5/8. Если −57/32 < β ≤ −7/4, то уравнение имеет два решения: х1 и х2 (которые, очевидно, различны); если −7/4 < β ≤ 12, то х1 и х3; а если β ≥ 12, то два решения: х1 и х2.
Корни х1 и х3 различны, так как −½ < х3 < 2, а х1 лежит вне этого интервала.
Ответ. β = −57/32.
9.11. Если x ≥ 0, y ≥ 0, то получим систему
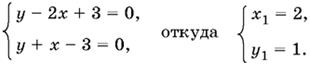
Если x ≥ 0, y ≤ 0, то
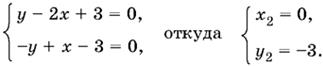
Если x ≤ 0, y ≥ 0, то
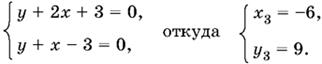
Если x ≤ 0, y ≤ 0, то
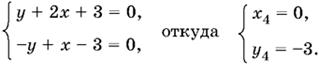
Каждое из четырех решений удовлетворяет записанным ограничениям.
Ответ. (2, 1); (0, −3); (−6, 9); (0, −3).
9.12. Исключая последовательно y и x, найдем
x = k + 16/7, y = 8 − 3k/7.
Остается решить систему неравенств
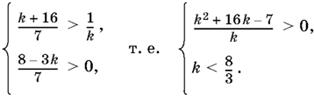
Первое неравенство равносильно такому:
(k + 8 + √71 )(k + 8 − √71 )k > 0.
Приходим к системе
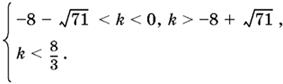
Так как −8 + √71 < 8/3, то условию задачи удовлетворяют два интервала.
Ответ. −8 − √71 < k < 0; −8 + √71 < k < 8/3.
9.13. Если x ≥ −у и x ≥ y, то получим системы
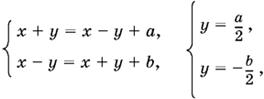
которая при x ≥ −у и x ≥ y имеет решение
x ≥ |a|/2, y = а/2
при условии а = −b.
Если x ≥ −у, но x ≤ y, то
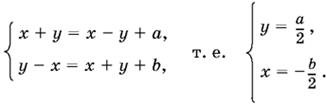
Из условия x ≥ −у находим −b/2 ≥ −а/2, а из второго условия: −b/2 ≤ а/2. Оба этих неравенства соответствуют условию а ≥ |b|.
Если x ≤ −у, а x ≥ y, то
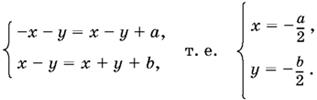
Подставляя найденные значения x и y в ограничения, получим b ≥ |а|.
Наконец, если x ≤ − у, x ≤ y, получим
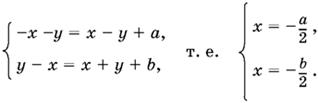
Это значит, что а = b. Так как y ≥ x, но y ≤ −х, то −x ≥ 0. Окончательно получим при а = b ≥ 0
x = −а/2, −а/2 ≤ y ≤ а/2.
Ответ. При а = −b, x ≥ |а|/2, y = а/2; при а ≥ |b|, x = −b/2, y = а/2; при b ≥ |a|, x = −а/2, y = −b/2; при а = b ≥ 0, x = −а/2, −а/2 ≤ y ≤ а/2.
9.14. Уравнение x² + y² = а при а < 0 не имеет решений. Если а ≥ 0, то это — уравнение окружности радиуса √a с центром в начале координат. Второе уравнение определяет стороны квадрата, диагонали которого равны 2 и расположены на осях координат (рис. P.9.14).
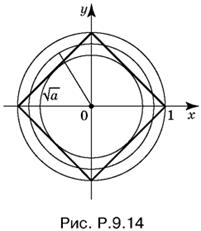
При увеличении а окружность будет увеличиваться и сначала окажется вписанной в квадрат, затем пересечет его в восьми точках и, наконец, будет описана около квадрата.
Итак, если √а < √2/2, то система не имеет решений.
Если √а = √2/2, т. е. а = ½, получим четыре решения: x = ½, y = ½ и три симметричных: (−½, ½), (−½, −½), (½, ½).
Если ½ < а < 1, то восемь решений. Мы найдем их, возведя первое уравнение в квадрат и получив с помощью второго уравнения, что |x| · |y| = 1 − a/2. B результате придем к системе
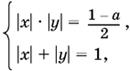
которая при положительных x и y имеет два решения:
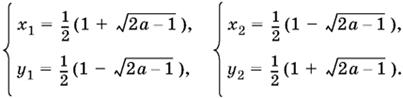
К этим решениям нужно добавить шесть симметричных.
Если а = 1, то y системы четыре решения: x1 = 1, y1 = 0; x2 = 0, y2 = 1; х3 = −1, у3 = 0; х4 = 0, у4 = −1. При а > 1 решений нет.
9.15. Если либо x = 0, либо y = 0, то второе неизвестное тоже равно нулю. Получаем очевидное решение
x1 = 0, y1 = 0.
Если ху ≠ 0, то можно первое уравнение разделить на ху, а второе — на x²y². Получим систему
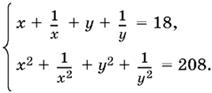
Введем обозначения:
x + 1/x = u, y + 1/y = v.
Возводя каждое из этих равенств в квадрат, получим x² + 1/x² = u² − 2, y² + 1/y² = v² − 2.
Система примет вид
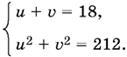
Решая ее, найдем: u1 = 4, v1 = 14; u2 = 14, v2 = 4. (Если первое уравнение возвести в квадрат и сравнить со вторым, то получим uv = 56.) Остается решить две системы:
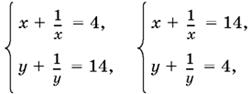
в результате чего получим восемь решений.
Ответ. (0, 0); (2 + √3, 7 + 4√3); (2 + √3, 7 − 4√3); (2 − √3 , 7 + 4√3 ); (2 − √3, 7 − 4√3 ); (7 + 4√3 , 2 + √3); (7 + 4√3, 2 − √3); (7 − 4√3, 2 + √3); (7 − 4√3, 2 − √3).
9.16. Способ 1. Из первого уравнения находим
y − z = ху − x.
Подставляя во второе, получим
xz = 2(x − ху + x), т. е. xz = 2x(2 − y).
Если x = 0, то система принимает вид

Получаем два решения системы:
x1 = 0, y1 = 0, z1 = 0;
x2 = 0, y2 = 6, z2 = 6.
Если x ≠ 0, то z = 2(2 − y). Подставляем во второе и третье уравнения
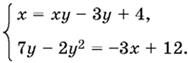
Подставим x из первого уравнения во второе:
7у − 2у² = −3ху + 9у.
Если y = 0, то получаем еще одно решение:
x3 = 4, y3 = 0, z3 = 4.
Если y ≠ 0, то 3x − 2y = 2, откуда x = 2(y + 1)/3. Подставляем в первое уравнение последней системы уравнение, которое превращается в квадратное относительно y:
2у² − 9у + 10 = 0,
откуда y4 = 2, y5 = 3 . Делаем проверку.
Способ 2. Запишем систему в виде
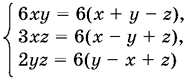
и сделаем три парных сложения
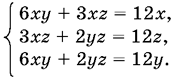
Отсюда находим решения:
а) x = y = z = 0;
б)
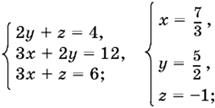
в) если x = 0, то
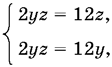
y = z = 6;
г) если y = 0, то
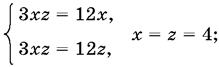
д) если z = 0, то
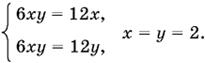
Ответ. (0, 0, 0); (0, 6, 6); (4, 0, 4); (2, 2, 0); ( 7/3, 5/2, −1).
9.17. Возведем уравнение x + y = −z в квадрат:
x² + y² + 2ху = z²,
и сравним со вторым уравнением системы; найдем ху = −10.
Преобразуем сумму x4 + y4 из третьего уравнения следующим образом:
x4 + y4 = (x² + y²)² − 2x²y² = (20 + z²)² − 200,
где на последнем шаге были использованы второе уравнение системы и найденное значение для ху. Подставив это выражение в третье уравнение системы, получим
z² = 9, т. е. z = ±3.
Остается решить каждую из систем:
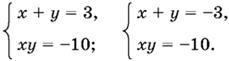
Производим проверку.
Ответ. (−2, 5, −3); (5, −2, −3); (2, −5, 3); (−5, 2, 3).
9.18. Третье уравнение можно записать так:
(x + y)(x² − ху + y²) + (z − 1)(z² + z + 1) = 0.
Из первого уравнения мы знаем, что x + y = 1 − z. Поэтому
(1 − z)(x² − ху + y² − z² − z − 1) = 0.
Если z = 1, то x + y = 0. Тогда из второго уравнения получим ху = −4. B итоге — два решения:
x1 = 2, y1 = −2, z1 = 1;
x2 = −2, y2 = 2, z2 = 1.
Если же 1 − z ≠ 0, то
x² − ху + y² − z² − z − 1 = 0. (3)
Чтобы упростить уравнение (3), снова воспользуемся тем, что x + y = 1 − z, а потому
x² + 2ху + y² = 1 − 2z + z². (4)
Вычитая уравнение (4) из уравнения (3), получим
ху = −z.
Теперь второе уравнение исходной системы
ху + z(x + y) = −4
можно переписать как уравнение относительно z
−z + z(1 − z) = −4.
Решая его, найдем, что либо z = −2, либо z = 2. B первом случае мы приходим к системе

Во втором случае получаем
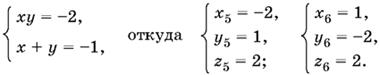
После того как были найдены первые два решения, решение системы можно было закончить следующим рассуждением.
Данная система симметрична относительно x, y и z. Поэтому одно ее решение (2, −2, 1) порождает 3! = 6 решений, получающихся в результате всевозможных перестановок. Таким образом, мы получим шесть различных решений системы.
С другой стороны, можно доказать, что система может иметь не больше решений, чем произведение степеней ее уравнений: 1 · 2 · 3 = 6. Поскольку все шесть решений найдены, решение системы можно считать законченным, если проверить одно из найденных решений.
Ответ. (2, −2, 1); (−2, 2, 1); (1, 2, −2); (2, 1, −2), (−2, 1, 2); (1, −2, 2).
9.19. Рассмотрим многочлен M(t) = (t − x)(t − y)(t − z) + d. Его корнями по условию являются не совпадающие друг с другом числа а, b и с, следовательно,
M(t) = (t − а)(t − b)(t − с), или (t − а)(t − b)(t − с) ≡ (t − x)(t − y)(t − z) + d.
Приравнивая коэффициенты при одинаковых степенях t, найдем
x + y + z = а + b + с = u,
ху + хz + уz = ab + ас + bc = v,
xyz = аbс + d = w
(справа указаны вводимые нами обозначения).
Поскольку нужно найти сумму x³ + y³ + z³, выразим ее через u, v и w, осуществив непосредственное возведение в куб суммы x + y + z = u:
u³ = x³ + y³ + z³ + 3uv − 3w (5)
(необходимые выкладки проведите самостоятельно). Запишем теперь то же соотношение для а + b + с = u и тем самым выразим а³ + b³ + с³ через u, v и w:
u³ = а³ + b³ + с³ + 3uv − 3(w − d). (6)
Вычитая из (6) соотношение (5), получим
x³ + y³ + z³ = а³ + b³ + с³ + 3d.
Ответ. а³ + b³ + с³ + 3d.
9.20. Умножив первое уравнение на ху²z², а второе — на x²уz², получим y первых двух уравнений равные правые части:
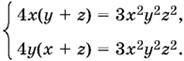
При этом могут быть получены посторонние решения, y которых одно из неизвестных обращается в нуль. Эти решения можно сразу отбросить, так как система в этом случае не удовлетворяется.
Сравним левые части полученных уравнений:
4z(x − y) = 0.
Так как z ≠ 0, то x = y. Из третьего уравнения системы получаем тогда z = 1/x³. Подставим эти значения y и x в первое уравнение:
4х4 + 1 = 0. (7)
Уравнение (7) не имеет действительных решений.
Ответ. Действительных решений нет.
9.21. Возведя второе уравнение в квадрат, найдем
(x + y)² = x²y²/4.
Подставим в первое уравнение
x4 + y4 = 17/4x²y², т. е. (x² − y²)² = 9/4x²y²,
откуда
x² − y² = ±3/2ху,
или, воспользовавшись вторым уравнением исходной системы, получим
x² − y² = ±3(x + y),
откуда
(x + y)(x − y ± 3) = 0.
Если x + y = 0, то и ху = 0, следовательно,
x1 = 0, y1 = 0.
Если x − y = 3, то, подставляя во второе уравнение данной системы y = x − 3, придем к уравнению x² − 7x + 6 = 0, с помощью которого найдем два решения системы:
x2 = 1, y2 = −2;
x3 = 6, y3 = 3.
Если же x − y = −3, то аналогично получим
x4 = −2, y4 = 1;
x5 = 3, y5 = 6.
Производим проверку.
Ответ. (0, 0); (1, −2); (6, 3); (−2, 1); (3, 6).
9.22. Умножим первое уравнение на t:
хt + уt = t
и вычтем из второго. Аналогично поступим со вторым и третьим уравнениями. Придем к системе, не содержащей y:
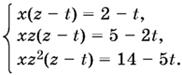
B результате могут быть получены посторонние решения, в которых t = 0. Однако решение нашей системы мы закончим проверкой, благодаря которой все посторонние решения будут отсеяны.
Если x = 0, то одновременно 2 − t = 0 и 5 − 2t = 0, что невозможно. По аналогичной причине z − t ≠ 0, z ≠ 0.
Поделим теперь второе уравнение последней системы на первое, а третье на второе. Получим
z = 5 − 2t/2 − t, z = 14 − 5t/5 − 2t.
Приравнивая эти выражения для z, придем к квадратному уравнению относительно t:
t² − 4t + 3 = 0, т. е. t1 = 1, t2 = 3.
Итак, z1 = 3, z2 = 1.
Остается определить x и y и сделать проверку.
Система имеет два решения.
Ответ. (½, ½, 3, 1) (½, ½, 1, 3).
9.23. Возведем первое уравнение в квадрат и вычтем из второго уравнения. После упрощения получим
2ху − 3хz + 6уz = 54.
Третье уравнение позволяет заменить 3xz на 4у²:
2ху − 4у² + 6уz = 54, или ху − 2у² + 3уz = 27. (8)
Вычтем из уравнения (8) первое уравнение системы, умноженное на y[17], получим
y = 3.
Подставим в первое и третье уравнения системы
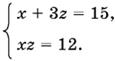
Решая эту систему, найдем два решения:
x1 = 3, z1 = 4; x2 = 12, z2 = 1.
Производим проверку.
Ответ. (3, 3, 4); (12, 3, 1).
9.24. Сложив первое уравнение со вторым, первое с третьим и, наконец, второе с третьим, получим систему
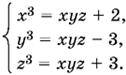
Перемножим эти уравнения и обозначим xyz = u:
u³ = (u + 2)(u² − 9),
а после упрощения
2u² − 9u − 18 = 0,
откуда u1 = 6, u2 = −3/2.
Для первого значения u находим x³ = 8, y³ = 3, z³ = 9, аналогично поступаем с u2. Производим проверку.
Ответ.
![]()
9.25. Обозначим x1 + x2 + ... + xn = s. Тогда уравнение, стоящее на месте с номером k, примет вид
xk(s − xk) + k(k + 1)s² = (2k + 1)²а²,
или
xk² − sxk − k(k + 1)s² + (2k + 1)²a² = 0,
откуда
![]()
Возьмем для всех xk знак минус и составим сумму х1 + ... + xn. Получим уравнение относительно в
![]()
откуда
![]()
Мы взяли перед корнем знак плюс, так как из уравнения для в видно, что s > 0; знаменатель не обращается в нуль ни при каких натуральных h.
Остается подставить найденное значение в в выражение для xk и сделать проверку.
Ответ.
![]()
9.26. Пусть 7x − 11у = u, т. е. 7(x + y) − 18у = u, откуда x + y = и + 18y/7, а x + 9у = (x + y) + 8у = и + 74y/7.
Приходим к системе
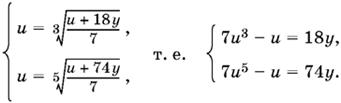
Из последней системы исключим y:
![]()
Если u = 0, то, как легко видеть, придем к очевидному решению: x1 = y1 = 0.
Если u ≠ 0, то получаем уравнение
![]()
откуда u1 = ⅓, u2 = −⅓, u3 = 2, u4 = −2.
Для каждого значения u составляем систему
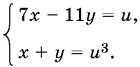
Делаем проверку.
Ответ. (0, 0); (10/243, −1/243); (−10/243, 1/243); (5, 3); (−5, −3).
9.27. Если сложить уравнения системы и вычесть из первого второе, получим систему:
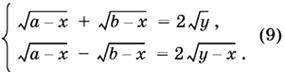
Возведем каждое из уравнений системы (9) в квадрат и вычтем из первого полученного уравнения второе. Получим
![]()
т. е.
(а − x)(b − x) = x², или (а + b)x = ab.
Если а + b = 0, но ab ≠ 0, то последнее уравнение, а следовательно, и данная система не имеют решений.
Если а + b = 0 и ab = 0, то а = b = 0. Написанная в начале решения система принимает вид
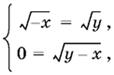
откуда y = −x и y = x одновременно, т. е. при а = b = 0 система имеет единственное решение x = y = 0.
Если а + b ≠ 0, то x = ab/a + b.
Из уравнения
![]()
находим y:
![]()
т. е.
![]()
откуда y = (|a| + |b|)²/4(a + b).
Так как а + b стоит в предпоследнем уравнении под радикалом и а + b ≠ 0, то а + b > 0.
Преобразовывая систему, мы получили уравнение
![]()
Следовательно, x ≥ 0, т. е. ab ≥ 0, а значит, и а ≥ 0, b ≥ 0.
Теперь можно записать, что
y = a + b/4.
Делаем проверку. Первое уравнение системы после подстановки примет вид
2а − |а − b| = а + b.
Если а ≥ b, то это уравнение удовлетворяется, а если а < b, то получим а = b, что противоречит предположению а < b.
Второе уравнение системы после подстановки дает равенство 2b + |а − b| = а + b.
При а ≥ b получаем тождество.
Ответ. Если а ≥ b ≥ 0 и а + b > 0, то x = ab/a + b, y = а + b/4; если а = b = 0, то x = y = 0.
9.28. Обозначим √у = z. Тогда система перепишется в виде
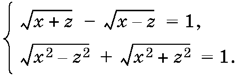
Дважды возведем первое уравнение в квадрат:
![]()
отсюда
![]()
далее
4z² = 4х − 1, или z² = x − ¼.
Заменив
![]()
выражением x − ½, перепишем второе уравнение системы так:
![]()
Из последнего уравнения находим z²:
z² = 9/4 − 3x,
и сравниваем с выражением для z², полученным из первого уравнения:
x − ¼ = 9/4 − 3x.
Отсюда x = 5/8, а y = z² = 3/8.
Проверяем найденные значения x и y. Левая часть первого уравнения системы примет вид
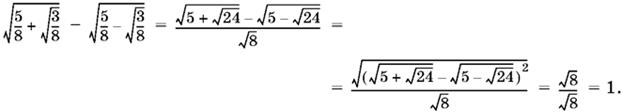
Левая часть второго уравнения вычисляется проще:
![]()
Ответ. (5/8, 3/8).
9.29. Способ 1. Так как а и b положительны, то из данных уравнений следует, что x > 0 и y > 0.
Возведем каждое из уравнений в квадрат:
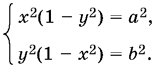
B результате могут быть приобретены только такие посторонние решения, при которых либо x < 0, либо y < 0.
Выражения 1 − y² и 1 − x², как это видно из последней системы, останутся положительными.
Мы получили систему относительно x² = u и y² = v:
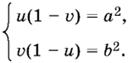
Чтобы эта система была равносильна предыдущей (при замене неизвестных равносильность может быть нарушена!), достаточно потребовать выполнения неравенств
u > 0, v > 0.
Раскрыв в последней системе уравнений скобки, получим
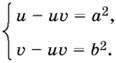
Вычитая из первого уравнения второе, найдем
u − v = а² − b²,
т. е. u = v + а² − b². Подставим в первое уравнение последней системы, получим квадратное уравнение относительно v:
v² + (а² − b² − 1)v + b² = 0,
откуда
![]()
Вычисляем u:
![]()
(У u и v, входящих в одно решение, берутся одноименные знаки.)
Подкоренное выражение можно преобразовать следующим образом:
(1 − а² + b²)² − 4b² = (1 − а² + b² − 2b)(1 − а² + b² + 2b) = [(1 − b)² − а²][(1 + b)² − а²] = (1 − b − а)(1 − b + а)(1 + b − а)(1 + b + а).
Так как а > b > 0 и а + b < 1, то каждый из четырех множителей положителен и дискриминант тоже положителен.
Если перед корнем выбран знак плюс, то u и v положительны. Докажем, что v > 0. Имеем а² − b² = (а − b)(а + b) < а − b < а − b + 2b = а + b < 1. Следовательно, 1 − а² + b² > 0 и, обращаясь к выражению для v, находим, что v > 0. Так как а > b, то очевидно, что и u > 0.
Если перед корнем выбран знак минус, то нужно проверить, что u и v положительны. Так как а > b, то проверку достаточно провести для v, которое меньше u.
Неравенство
![]()
очевидно.
Нетрудно проследить, что в процессе решения системы уравнений относительно u и v при условии, что u и v положительны, мы не нарушали равносильности.
Способ 2. Эту систему естественно было бы решать с помощью подстановки x = sin φ, y = sin ψ, где 0 < φ < π/2, 0 < ψ < π/2. Такая подстановка возможна, поскольку из имеющихся в условии ограничений легко получить, что 0 < x < 1, 0 < y < 1. Получим систему
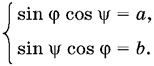
Складывая и вычитая уравнения этой системы, найдем
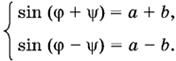
Так как по условию 0 < а + b < 1 и 0 < а − b < 1, а на φ и ψ были наложены ограничения 0 < φ < π/2, 0 < ψ < π/2, то можно написать

или
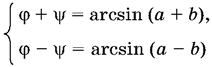
Из первой системы получим
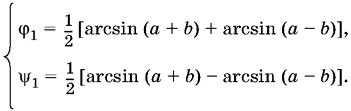
Найдем sin φ1 и sin ψ1:
![]()
где α = arcsin (а + b), β = arcsin (а − b). (При выборе знаков перед корнями мы здесь и в дальнейшем принимаем во внимание ограничения на φ и ψ: 0 < φ < π/2, 0 < ψ < π/2.) Продолжим преобразования:
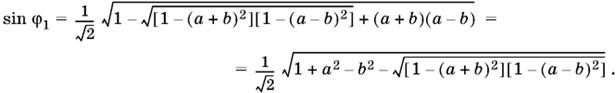
Нетрудно убедиться в том, что
[1 − (а + b)²][1 − (а − b)²] = (1 − а² + b²)² − 4b².
Аналогично найдем sin ψ1, а также sin φ2 и sin ψ2.
Ответ. Если а > b > 0, а + b < 1, то система имеет два решения:
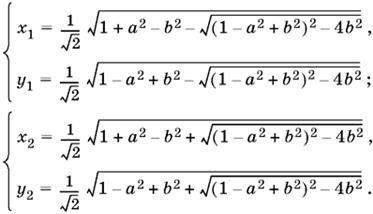
9.30. Наряду с решением x1, y1, z1 система обязательно имеет решение −х1, −у1, z1. Поэтому у системы будет единственное решение только в том случае, когда x = y = 0.
Подставляя x = y = 0 в исходную систему, получим
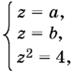
откуда либо а = b = 2, либо а = b = −2.
Проверим, действительно ли при найденных значениях а и b система имеет единственное решение.
Если а = b = 2, то из первого уравнения находим
xyz = 2 − z.
Подставляя во второе, получим квадратное уравнение относительно z:
z² − 3z + 2 = 0,
корни которого z1 = 1, z2 = 2.
При z = 1 получим систему
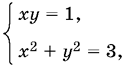
которая, как легко проверить, имеет четыре решения.
Таким образом, значения параметров а = b = 2 не удовлетворяют условию задачи.
Если а = b = −2, то из первого уравнения найдем
xyz = −2 − z.
Подставляем во второе:
z² + z − 2 = 0,
откуда z1 = −2, z2 = 1.
При z = −2 приходим к системе
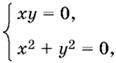
имеющей единственное решение x = y = 0. При z = 1 получаем систему
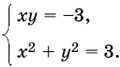
Подставляем во второе уравнение y = −3/x и убеждаемся, что уравнение x4 − 3x² + 9 = 0, которое получается в результате, имеет только мнимые корни.
Ответ. a = b = −2.
9.31. По условию y = −x. Данные уравнения примут вид
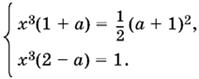
Если а ≠ −1, то, найдя x³ из первого и второго уравнений, приравняем полученные выражения
½(а + 1) = 1/2 − a, т. е. а² − а = 0,
откуда а = 0 или а = 1.
Условию задачи могут удовлетворить только три значения параметра а:
−1, 0, 1,
которые нужно проверить.
Если а = −1, то из первого уравнения найдем y = −x, а из второго уравнения найдем x³ = ⅓ и
![]()
, а следовательно,
![]()
Найденные значения неизвестных удовлетворяют и условию x + y = 0.
Если а = 0, то из первого уравнения:
![]()
а из второго:
![]()
Это значит, что при а = 0 система имеет два решения:
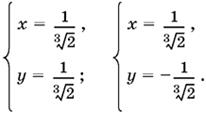
По условию любое решение должно удовлетворять требованию x + y = 0, между тем первое решение этому требованию не удовлетворяет. Значение а = 0 мы должны отбросить.
Осталось рассмотреть случай, когда а = 1. B этом случае получим систему
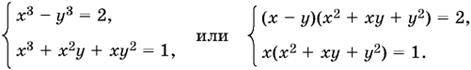
Так как правые части отличны от нуля, то разделим первое уравнение на второе, откуда x + y = 0. Поскольку условие x + y = 0 теперь автоматически выполняется для любого решения системы, то нужно убедиться, что y этой системы есть хотя бы одно решение. Таким решением является x = 1, y = −1. (Докажите.)
Ответ. ±1.
9.32. Так как система должна иметь хотя бы одно решение при любом b, то она должна иметь решение и при b = 0. Положив b = 0, получим систему
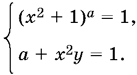
Первое уравнение удовлетворяется либо при а = 0 и любом x, либо при x = 0. Если x = 0, то из второго уравнения получаем а = 1. Итак, возможны только два значения: а = 0 и а = 1.
При а = 0 получаем систему
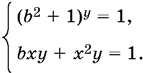
Первое уравнение имеет решение при любом b, только если y = 0. Однако это значение y не удовлетворяет второму уравнению.
Остается рассмотреть случай а = 1. Система примет вид
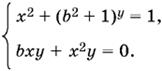
При любом b эта система имеет решение x = y = 0.
Ответ. 1.
9.33. Пусть (х1, у1) — решение системы. Тогда второе уравнение удовлетворяется еще тремя парами значений неизвестных (−x1, y1), (x1, −y1), (−x1, −y1). Легко убедиться, что первое уравнение наряду с (x1, y1) имеет также решение (x1, −y1):
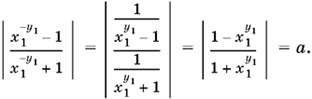
Таким образом, система может иметь единственное решение лишь при условии, что y1 = −y1, т. е. y = 0. Подставим это значение y в систему. Из первого уравнения получим а = 0.
Выясним, достаточно ли условия а = 0 для единственности решения исходной системы. Если а = 0, то xy = 1, а это означает, что либо x = 1, y — любое число, либо x ≠ 0 — любое, y = 0. Значения параметра b должны быть такими, чтобы второму уравнению системы удовлетворяло только одно из решений первого. Если y = 0, то второе уравнение имеет единственное решение x = √b (по условию x > 0) при любом b > 0. Поэтому b нужно выбрать таким, чтобы исключить случай x = 1, т. е. таким, чтобы уравнение 1 + y² = b не имело действительных решений. Для этого необходимо и достаточно выполнение ограничения b < 1.
Если x = 1, то второе уравнение имеет единственное решение в том и только в том случае, если b = 1. При этом ему удовлетворяет единственное из решений первого уравнения: x = 1, y = 0.
Ответ. а = 0, 0 < b ≤ 1.
9.34. Умножим числитель и знаменатель дроби из второго уравнения на
![]()
Полученное уравнение разделим на y, который тоже отличен от нуля, если входит в решение системы. Получим
![]()
Исключим
![]()
с помощью первого уравнения системы:
x²/y² − 2x/y + y² + 2x − 2y = 3.
Последнее уравнение перепишем в виде
x²/y² + 2x + y² − 2(x/y + y) = 3
Если x + y = z, то z² − 2z − 3 = 0, z1 = −1, z2 = 3. Первое уравнение данной системы можно записать в виде
![]()
Если
![]()
откуда x = 0. Второе уравнение системы дает тогда два значения: y1 = 0, y2 = −1, где y = 0 не удовлетворяет первому уравнению. Если z = 3, то x = 4/3; второе уравнение системы после несложных преобразований принимает вид 3y²+ y + 4 = 0, т. е. не имеет действительных решений.
Проверка убеждает нас в том, что x = 0, y = −1 — единственное решение системы.
Ответ. (0, −1).
9.35. Запишем данное уравнение в виде
|6 − |x − 3| − |x + 1|| = а(x + 5) + 4. (10)
Построим график функции
y = |6 − |x − 3| − |x + 1||. (11)
Начнем с графика функции
y = 6 − |x − 3| − |x + 1|, (12)
который легко построить, разбив числовую ось на три интервала точками x = −1, x = 3 (рис. P.9.35).
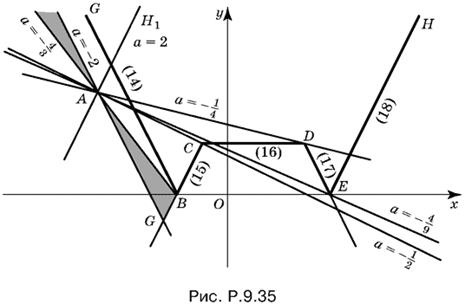
Получим
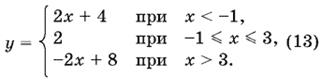
Этот график совпадает с графиком функции (11) там, где значения y, полученные из (13), неотрицательны. Если же значения y, полученные из (13), отрицательны, то им соответствуют симметричные относительно оси Ox точки графика. Таким образом, для интервала −2 ≤ x ≤ 4 графики функций (11) и (12) совпадают, а при x < −2 и при x > 4 мы получаем симметричные относительно оси Ox лучи. В итоге для функции (11) имеем:

График этой функции изображен на рис. P.9.35 жирной линией (около каждого отрезка указан номер соответствующего ему уравнения).
Если подойти к задаче формально, то мы можем рассчитать точки пересечения прямой (19) — см. ниже — с каждой из прямых (14), (15), (16), (17), (18). Получим соответственно:
x1 = −5a + 8/a + 2, x2 = 5a/2 − a, x3 = −5a + 2/a, x4 = 4 − 5a/a + 2, x5 = 5a + 12/2 − a.
Рассмотрим теперь при разных значениях параметра а семейство прямых
y = а(x + 5) + 4 (19)
и определим, сколько точек пересечения y каждой из прямых (19) с графиком функции (13).
Тангенс угла наклона прямых (19) равен а и все эти прямые проходят через точку А(−5; 4). Обозначим на графике точки В(−2; 0), С(−1; 2), D(3; 2), E(4; 0), а также точки G и H, расположенные на левом и правом лучах графика (11) соответственно. Соединим точку А(−5; 4) с точками /(−2; 0), С(−1; 2), 1(3; 2) и E(4; 0). Проведем через точку А прямые AG1 || EH. Обозначим на каждой из проведенных нами через точку А прямых ее угловой коэффициент а: для AC имеем а = −2, для AB, AC, AE, AD и AH1 соответственно а принимает значения: −4/3, −½, −4/9, ¼, 2.
Теперь нетрудно подсчитать, при каких а какие решения имеет данное в условии уравнение. Получим
одно решение x1 при а < −2;
решений нет при −2 ≤ а < −4/3;
одно решение x1 = x2 при а = −4/3;
два решения x1, x2 при −4/3 < а < −½;
два решения x1, x2 = x3 при а = −½;
два решения x2, x3 при −½ < а < −4/9;
три решения x1, x3, x4 = x5 при а = −4/9;
четыре решения x1, x3, x4, x5 при −4/9 < а < −¼;
три решения x1, x3 = x4, x5 при а = −¼;
два решения x1, x5 при −¼ < а < 2;
одно решение x1 при а ≥ 2.
Замечание: при а = −2 решений нет, а при а = 2 есть единственное решение x1, которое при а = 2 существует.
9.36. После возведения в квадрат и приведения подобных можно утверждать, что уравнение равносильно системе
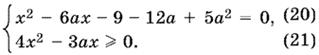
Дискриминант уравнения (20) равен 4a² + 12a + 9 = (2a + 3)². Он неотрицателен. Уравнение имеет один корень x = 3a при а = −3/2 и два корня x1,2 = 3a ± |2a + 3| при остальных а.
Если а = −3/2, то x = −9/2. При этих значениях а и x неравенство (21) удовлетворяется.
Пусть а < −3/2. Тогда |2a + 3|= −2a − 3, т. е. x1 = 5а + 3, x2 = а − 3. Для каждого из этих корней решим неравенство (21) и учтем ограничение а < −3/2 . Пусть сначала x1 = 5а + 3, тогда:
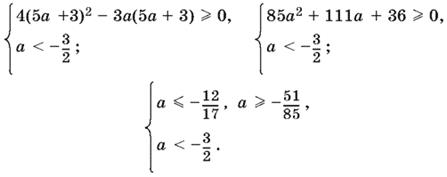
Решением последней системы будет а < −3/2, т. е. корень x1= 5а + 3 существует при всех а < −3/2.
Пусть теперь x2 = а − 3, тогда:
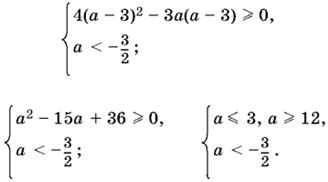
Итак, корень x2 = а − 3 существует при всех а < −3/2.
Таким образом, при а < −3/2 исходное уравнение имеет два корня x1 = 5а + 3 и x2 = а − 3.
Аналогично исследуется случай а < −3/2. При этом |2a + 3| = 2a + 3 и соответственно x1 = 3a − (2a + 3); x2 = 3a + (2a + 3) = 5а + 3. Подставляем эти значения в (21). Для x1 = а − 3 получим:
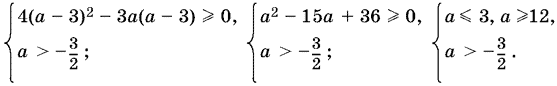
Аналогично для x2 = 5а + 3 имеем:
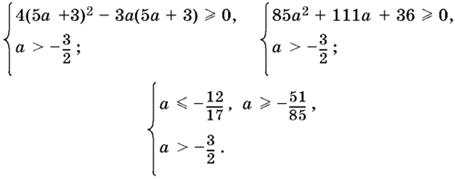
Итак, x1 = а − 3 будет корнем исходного уравнения, когда
−3/2 < а ≤ 3 и а ≥ 12.
x2 = 5а + 3 будет корнем, когда −3/2 < а ≤ −12/17; а ≥ −51/85.
Обобщим результаты на числовой оси а (рис. P.9.36).
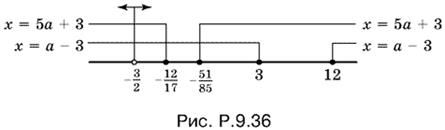
Ответ. При a ∈ (−∞, −3/2) ∪ (−3/2, −12/17) ∪ (−51/85, 3) ∪ [12, +∞) уравнение имеет два корня: x1 = 5а + 3, x2 = а − 3. При а = −3 имеет один корень x = 3a = −9/2. При а ∈ (−12/17, −51/85) уравнение имеет один корень x = а − 3, а при а ∈ (3, 12) — один корень x = 5а + 3.
9.37. Уравнение можно записать в виде
x(5x/5x² − 7x + 6 + 2x/5x² − x + 6 − 1) = 0.
При x = 0 множитель в скобках существует и равен −1. Поэтому x = 0 — корень данного уравнения. Другие корни должны быть корнями уравнения
5x/5x² − 7x + 6 + 2x/5x² − x + 6 = 1. (22)
В знаменателях стоят симметрические многочлены. Значение x = 0 не является корнем (22) и выражение (22) не теряет при этом значении смысла. Поэтому разделим числители и знаменатели каждой дроби на x:
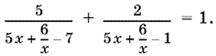
Проведем замену
t = 5х + 6/x. (23)
Тогда
5/t − 7 + 2/t − 1 = 1. (24)
Дальше решение стандартно. Уравнение (24) имеет корни t1 = 13 и t2 = 2. Подставляя их в (23), найдем для t1 значения x2 = 2, x3 = 3/5. Для t2 решений нет.
Ответ. 0; 2; 3/5.
9.38. Пусть x + y = u, xy = v. Тогда получим
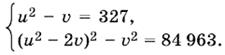
Во второе уравнение подставим u² = v + 327:
(327 − v)² − v² = 84 693,
или
327² − 2 · 327v = 84 963.
Так как 84 693 = 327 · 259, то сократим уравнение на 327 и найдем v = 34, u² = 361.
Остается решить две системы:
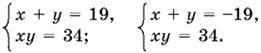
Ответ. (2, 17), (17, 2), (−2, −17), (−17, −2).