Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Алгебраические неравенства
Ответы к упражнениям на с. 59, 62 и 63.
1. Получим совокупность неравенств, имеющую те же самые решения.
2. Получим систему неравенств, не имеющую решений.
3. Ответ. −1 < x ≤ 1, 5 < x ≤ 7, x > 8.
4. Вначале нужно переписать неравенство в виде
(x − 5/2)(zx − 3)(x − 4)² ≤ 0.
Последний множитель показывает, что точка 4 обязательно должна принадлежать множеству решений, этим его влияние ограничивается.
Ответ. 5/2 ≤ x ≤ 3, x = 4.
5. Поскольку неравенство строгое, то множители, стоящие в знаменателе, и множители, стоящие в числителе, играют одинаковую роль. Данное неравенство равносильно такому:
(x + 3)²(x + 1)(x − 2)(x − 4)²(x − 5) < 0.
Достаточно решить неравенство
(x + 1)(x − 2)(x − 5) < 0
и исключить, если они попали в множество решений, точки x = −3, x = 4.
Ответ. x < −3, −3 < x < −1, 2 < x < 4, 4 < x < 5.
6. 0 ≤ ax² + bх + с < 9.
7. ax² + bх + с ≥ 9; здесь не нужно заботиться о знаке подкоренного выражения, так как после возведения в квадрат получаем неравенство, из которого следует, что это выражение положительно.
8.
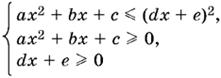
(см. пример 4 на с. 62).
9. Нужно разобрать два случая в зависимости от знака правой части: если правая часть отрицательна, то неравенство удовлетворяется при всех x, при которых левая часть существует; если правая часть неотрицательна, то обе части неравенства нужно возвести в квадрат (подкоренное выражение при этом не может стать отрицательным):
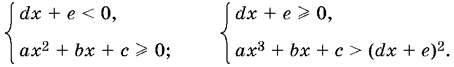
10.1. Обозначим а = 1 + k. Тогда из условия а + b = 2 получим b = 1 − k. Вычислим а4 + b4:
а4 + b4 = (1 + k)4 + (1 − k)4 = 2k4 + 12k² + 2 = 2(k4 + 6k² + 1) ≥ 2,
так как k4 + 6k² ≥ 0 и, следовательно, k4 + 6k² + 1 ≥ 1.
10.2. Обозначим произведение, стоящее в левой части неравенства, через P. Так как а1а2 ... аn = 1, то
![]()
(осуществлено почленное деление суммы 1 + аi на аi). Поскольку
![]()
то P² ≥ 4n и, следовательно, P ≥ 2n, что и требовалось доказать.
10.3. Способ 1.
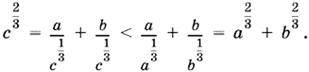
Способ 2. Неравенству a⅔ + b⅔ > c⅔ эквивалентно неравенство
(a/c)⅔ + (b/c)⅔ > 1.
Так как b < с и а < с, то основания показательных функций (a/c)x и (b/c)x меньше единицы и эти функции убывают. Следовательно,
(a/c)⅔ + (b/c)⅔ > a/c + b/c = 1.
10.4. Данное неравенство можно переписать так:
4x³ − 4x² + 1 ≥ 0.
Оценим левую часть:
4x²(x − 1) + 1 = −4x²(1 − x) + 1.
Так как 0 ≤ x ≤ 1, то x² ≤ x и 1 − x ≥ 0. Следовательно,
−4x²(1 − x) + 1 ≥ −4x(1 − x) + 1 = (2x − 1)² ≥ 0,
что и доказывает наше неравенство.
10.5. Каждый из входящих в неравенство корней оценим следующим образом:
![]()
Складывая полученные неравенства, придем к выводу, что
![]()
Теперь, чтобы доказать написанное в условии неравенство, остается убедиться, что в последней оценке равенство никогда не достигается. Равенство возможно лишь при одновременном выполнении равенств 4a + 1 = 1, 4b + 1 = 1, 4с + 1 = 1, т. е. при а = b = с = 0, что противоречит условию а + b + с = 1.
Итак,
![]()
10.6. Пусть b < а. Тогда
(а + b)n ≤ (2a)n = 2nan < 2n(an + bn).
10.7. Так как ( а/b)x − возрастающая показательная функция (по условию а > b) и p > q, то
![]()
Воспользовавшись формулой производной пропорции, получим
![]()
что и требовалось доказать.
10.8. Имеем n очевидных неравенств:
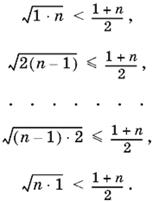
Первое и последнее неравенства обязательно будут строгими, так как по условию n > 1. Перемножая эти неравенства, получим
![]()
10.9. Способ 1. Обозначим a/b = u, b/c = v, c/a = w. Тогда uvw = 1, т. е. среди чисел u, v и w есть хотя бы одно, большее 1, и одно, меньшее 1 (u = v = w невозможно, так как а, b и с не равны друг другу). Пусть u > 1, а 0 < v < 1, т. е.
(1 − u)(v − 1) > 0 или −uv + u + v − 1> 0.
С другой стороны, для чисел u, v и e выполняется неравенство
![]()
т. е. uv + w ≥ 2. Складывая это неравенство с неравенством − uv + u + v − 1 > 0, получим
u + v + w > 3, или a/b + b/c + c/a > 3.
Способ 2. Пусть u, v и w — положительные числа, причем w — наименьшее из них: u > w, v > w. Так как u и w — положительные числа, то на них можно умножить неравенство v > w:
v(u − w) > w(u − w), т. е. uv − vw + w² > uw.
Поделим последнее неравенство на uw:
v/w − v/u + e/u > 1.
С другой стороны,
u/v + v/u ≥ 2.
Складывая с предыдущим неравенством, получим
u/v + v/w + w/u > 3.
Если с — наименьшее из чисел а, b и с, то полагаем w = с, u = а, v = b и получаем неравенство, которое требовалось доказать. Если а или b — наименьшее из чисел а, b и с, то обозначения соответственно изменятся.
Способ 3. Пусть b = с + d1, а = b + d2 (d1 > 0, d2 > 0, т. е. а > b > с). Тогда
![]()
Это решение обобщается на случай n чисел:
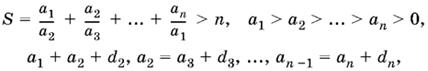
т. е.
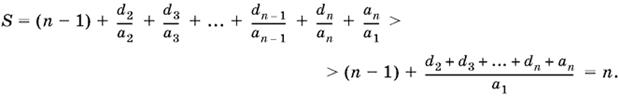
10.10. Воспользуемся формулой Герона и применим к сомножителям p − а, p − b, p − с неравенство между средним геометрическим и средним арифметическим трех чисел (p − а + p − b + p − с = 3p − 2p = p):
![]()
В условие входит величина 4S, для которой мы и проведем дальнейшие оценки
![]()
Выделим в числителе слагаемое 3(а² + b² + с²), а излишек в 2(а² + b² + с²) используем для образования полных квадратов, которые поглотили бы все попарные произведения:
![]()
и тем самым неравенство доказано.
10.11. Оценим левую часть неравенства:
(x − 1)(x − 3)(x − 4)(x − 6) + 10 = (х² − 7х + 6)(х² − 7х + 12) + 10 = [(х² − 7х + 9) − 3][(х² − 7х + 9) + 3] + 10 = (х² − 7х + 9)² − 9 + 10 = (х² − 7х + 9)² + 1 ≥ 1.
10.12. Подставляя в первое уравнение x² вместо yz, преобразуем систему следующим образом:
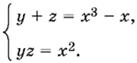
Числа y и z являются корнями квадратного уравнения относительно u:
u² + (x − х³)u + x² = 0.
По условию числа x и z действительные. Следовательно, дискриминант
D = (x − x³)² − 4x² = x²(1 − x²)² − 4x² = x²[(1 − x²)² − 4]
должен быть неотрицательным.
Так как по условию x ≠ 0, то
(1 − x²)² ≥ 4.
Это неравенство может выполняться, если либо 1 − x² ≤ −2, либо 1 − x² ≥ 2. Второе неравенство не имеет решений, а из первого получаем x² ≥ 3, что и требовалось доказать.
10.13. Перепишем данные уравнения в виде откуда
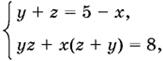
yz = 8 − x(5 − x).
Числа y и z будут корнями уравнения
u² − (5 − x)u + x² − 5х + 8 = 0.
Так как y и z должны быть действительными числами, то дискриминант этого уравнения не может стать отрицательным ни при каких значениях x:
(5 − x)² − 4(х² − 5х + 8) ≥ 0, т. е. −3x² + 10x − 7 ≥ 0,
откуда
1 ≤ x ≤ 7/3.
Так как уравнения, которым удовлетворяют x, y и z, симметричны, то аналогичные ограничения получим для y и z:
1 ≤ y ≤ 7/3, 1 ≤ z ≤ 7/3,
что и требовалось доказать.
10.14. Дискриминант квадратного трехчлена равен 1 − 4а. Если а < ¼, то дискриминант положителен и уравнение ax² + x + 1 = 0 имеет два различных корня:
![]()
Когда а > 0, т. е. 0 < а < ¼, то получим решения неравенства:
x < x1, x > x2.
Когда а < 0, то легко проверить, что x2 < x1. Поэтому решения запишутся в виде
x2 < x < x1.
Дискриминант отрицателен, когда а > ¼, а следовательно, а > 0. Неравенство удовлетворяется при всех x.
Если а = ¼, то решения неравенства запишутся в виде x ≠ −2.
10.15. Условия задачи выполняются тогда и только тогда, когда интервал 1 < x < 2 будет расположен между корнями параболы, т. е. если
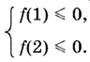
Подставляя значения 1 и 2 в данный трехчлен, получим систему двух квадратных неравенств
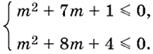
Решая первое неравенство, найдем
−7 − 3√5/2 ≤ m ≤ −7 + 3√5/2,
а решая второе, получим
−4 − 2√3 ≤ m ≤ −4 + 2√3.
Ответ. −½(7 + 3√5) ≤ m ≤ −4 + 2√3.
10.16. Пусть x1 и x2 — корни данного трехчлена. Тогда
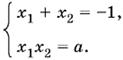
Если корни x1 и x2 действительны, то из первой формулы следует, что они не могут быть оба положительными. Если оба корня отрицательны, то из второй формулы находим а > 0, а следовательно, корни x1 и x2 меньше а. Если а = 0, то один из корней равен −1, и условие задачи снова не выполняется. Таким образом, а < 0. При а < 0 дискриминант 1 − 4a положителен и оба корня действительные. Потребуем, чтобы меньший из них был больше а, т. е.
![]()
Это неравенство эквивалентно такому:
![]()
Возведя обе части неравенства в квадрат, мы должны позаботиться о сохранении связей, которые неявно присутствуют в этом неравенстве:
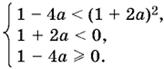
Последнее неравенство выполняется, так как мы установили, что а < 0. Первые два преобразуются к виду
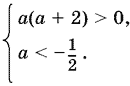
Ответ. а < −2.
10.17. Так как k ≠ 0, то ветви параболы направлены вверх. Внутри интервала от −1 до +1 парабола имеет только один корень тогда и только тогда, когда на концах этого интервала трехчлен имеет разные знаки, т. е.
(k² − k − 2)(k³ + k − 2) < 0.
Разлагая каждый из трехчленов на множители, получим
(k − 2)(k + 1)(k + 2)(k − 1) < 0.
Ответ. −2 < k < −1; 1 < k < 2.
10.18. Условие, что ветви параболы направлены вверх, означает, что m > 0. Если парабола не пересекает ось Ox, то получаем систему
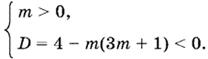
Если же данный квадратный трехчлен имеет действительные корни, то больший корень не должен быть положительным:
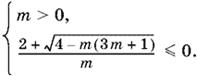
Второе неравенство второй системы (а следовательно, и вся система) не имеет решений при m > 0, так как числитель и знаменатель оказываются положительными.
Решая второе неравенство первой системы, найдем
m < −4/3, m > 1.
Принимая во внимание первое неравенство, находим решение системы: m > 1.
Пусть теперь m = 0. Правая часть данного неравенства принимает вид −4x + 1 > 0, т. е. x < ¼, и неравенство удовлетворяется не при всех положительных x.
Ответ. m > 1.
10.19. Неравенство равносильно совокупности двух систем
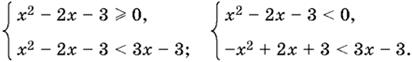
Решая каждое из четырех неравенств, придем к новой совокупности двух систем:
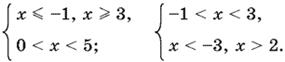
Итак, 3 ≤ x < 5, 2 < x < 3.
Ответ. 2 < x < 5.
10.20. Неравенство можно переписать в виде
(x − 3)² > (x + 2)²,
откуда после раскрытия скобок и приведения подобных получим линейное неравенство.
Ответ. x < ½.
10.21. При x > 0 неравенство можно переписать в виде
![]()
Последнее неравенство равносильно системе
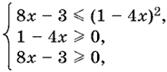
которая несовместна, так как несовместны два последних неравенства.
При x < 0 входящее в данное неравенство выражение
![]()
не существует.
Ответ. Неравенство не имеет решений.
10.22. Данное неравенство можно переписать так:
![]()
Получаем совокупность двух систем
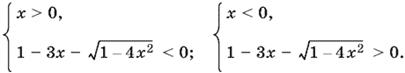
Решаем первую систему
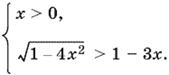
Если правая часть второго неравенства отрицательна (x > ⅓), то неравенству будут удовлетворять все x, при которых подкоренное выражение неотрицательно (x² ≤ ¼, |x| ≤ ½). Получаем интервал решений ⅓ < x ≤ ½.
Если правая часть второго неравенства неотрицательна (x ≤ ⅓), то второе неравенство можно возвести в квадрат (дополнять систему условием 1 − 4x² ≥ 0 или |x| ≤ ⅓ не нужно). После простых преобразований получим
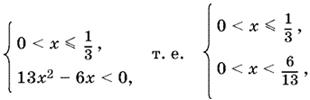
откуда 0 < x ≤ ⅓. Объединяя интервалы 0 < x ≤ ⅓ и ⅓ < x ≤ ½, получим решение первой системы: 0 ≤ x ≤ ½.
Перейдем ко второй системе:
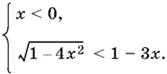
Условие x < 0 обеспечивает положительность правой части второго не равенства. Возведем второе неравенство в квадрат, учитывая, что |x| ≤ ½. Получим
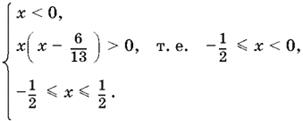
Ответ. −½ ≤ x < 0, 0 < x ≤ ½.
10.23. Перепишем данное неравенство в виде
![]()
Так как в неравенство входит выражение
![]()
а потому
![]()
. Вынесем множитель
![]()
за скобки:
![]()
Это неравенство равносильно системе
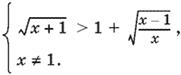
Возведем первое неравенство системы в квадрат. При этом следует добавить условие, в силу которого выражение, «освободившееся» от влияния радикала, должно быть неотрицательным:
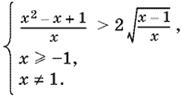
Так как x² − x + 1 > 0 при всех x, то первому неравенству системы могут удовлетворять только x > 0, ибо выражение справа всегда положительно. Следовательно, систему можно переписать в виде
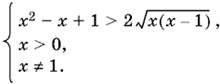
Обозначим
![]()
тогда первое неравенство примет вид y² − 2y + 1 > 0, т. е. (y − 1)² > 0, откуда y ≠ 1. Итак,
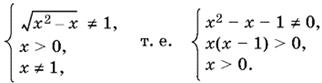
Последняя система равносильна такой:
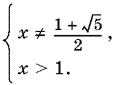
Ответ.
![]()
10.24. При x > 0 правая часть неравенства положительна, так как в этом случае
![]()
Возведем обе части неравенства в квадрат; получим систему
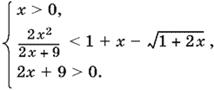
Последнее неравенство системы — следствие того, что x > 0. Перенесем во втором неравенстве 1 + x в левую часть и произведем некоторые упрощения. Получим систему
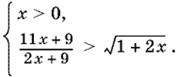
Так как x > 0, то второе неравенство можно возвести в квадрат, не добавляя при этом никаких ограничений (убедитесь в этом самостоятельно):
121x² + 198x + 81/4x² + 36x + 81 > 1 + 2x.
Умножим неравенство на знаменатель, который при x > 0 положителен; после приведения подобных получим систему
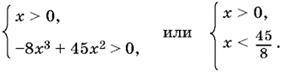
Итак, в первом случае неравенство имеет решения: 0 < x < 45/8.
При x = 0 данное неравенство не удовлетворяется.
Если же x < 0, то, умножив обе части на −1, придем к неравенству
![]()
Проделав с этим неравенством преобразования, аналогичные случаю, когда x > 0, придем к выводу, что оно не имеет решений при отрицательных x.
Ответ. 0 < x < 45/8.
10.25. Перепишем данное неравенство в виде
![]()
т. е.
![]()
Обозначив выражение, стоящее в скобках, через y, получим квадратное неравенство
y² + y − 42 < 0,
которое имеет решения: −7 < y < 6. Итак,
![]()
Поскольку сумма
![]()
всегда положительна, то достаточно решить лишь правое неравенство:
![]()
После возведения в квадрат получим неравенство
![]()
равносильное исходному, так как корни √x и
![]()
здесь не устранены. (Заметьте, что, заменив выражение √x
![]()
на
![]()
мы могли нарушить равносильность.) После второго возведения в квадрат придем к системе
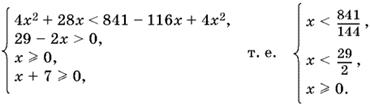
![]()
Ответ. 0 ≤ x < 841/144.
10.26. Неравенство удобно переписать в виде
![]()
Оно равносильно совокупности двух систем
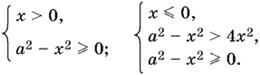
Решая последнее неравенство каждой из систем, найдем −|а| ≤ x ≤ |а|.
Так как в первой системе x > 0, то для нее получим решения:
0 < x ≤ |а|, а ≠ 0.
Перейдем ко второй системе. Решая второе неравенство, получим
−|а|/√5 < x < |а|/√5.
Мы приходим к системе
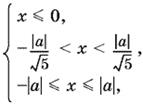
решениями которой будут значения из интервала −|а|/√5 < x ≤ 0 при а ≠ 0. Остается объединить решения двух систем.
Ответ. При а ≠ 0: −|а|/√5 < x ≤ |а|; при а = 0 неравенство не имеет решений.
10.27. Приведем степени, входящие в данное неравенство, к основанию 2 и поделим на 2√x 2x:
2x − √x ≤ 3 + 4 · 2√x − x;
обозначив 2x − √x = y, получим
y ≤ 3 + 4/y,
а так как y > 0, то
y² − 3y − 4 ≤ 0.
Корни трехчлена: −1, 4; так как меньший корень отрицателен, то получаем
2x − √x ≤ 4,
т. е. x − √x ≤ 2. Обозначим √x = z и найдем решения неравенства
z² − z − 2 ≤ 0.
Получим −1 ≤ z ≤ 2. Левое неравенство выполняется, если только √x существует. Остается √x ≤ 2, т. е. 0 ≤ x ≤ 4.
Ответ. 0 ≤ x ≤ 4.
10.28. Перепишем неравенство в виде
3√x(3 + x − 2x²) − 2(−2x² + x + 3) < 0,
или
(3√x − 2)(−2x² + x + 3) < 0.
Последнее неравенство[20] равносильно совокупности систем
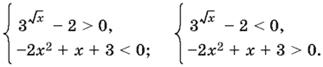
Решая первую систему, получим
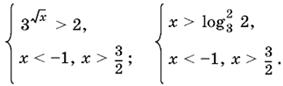
Так как −1 <
![]()
<
![]()
= 1 < 3/2, то окончательно получим x > 3/2.
Вторая система дает нам следующее:

Ответ.
![]()
10.29. Если x > 0, то неравенство равносильно такому:
(x − 1)2x − 1/3 − x < 0, т. е. (x − 1)(x − ½)/x − 3 > 0.
Воспользовавшись методом интервалов, получим ½ < x < 1, x > 3. Если x = 0, то левая часть неравенства обращается в выражение 0−⅓ , которое не имеет смысла.
При x < 0 показатель степени должен быть целым числом, т. е. 2x − 1/3 − x, откуда x(2 + n) = 3n + 1. Так как при n = −2 последнее уравнение не удовлетворяется, то
x = 3n + 1/2 + n.
Из условия x < 0 находим x = 3n + 1/2 + n < 0 и, следовательно, −2 < n < −⅓. Единственное целое число в этом интервале n = −1, а соответствующее ему значение неизвестного x = −2. Проверяем это значение, подставляя его в первоначальное неравенство: (−2)−1 < 1.
Ответ. x = −2, ½ < x < 1, x > 3.
10.30. Предположим, что основание больше единицы, т. е. 4x² + 12x + 10 > 1, или (2x + 3)² > 0. Это имеет место при всех x, кроме x = −3/2. При x = −3/2 основание равно единице, и, следовательно, исходное неравенство удовлетворяется. Если же x ≠ −3/2, то оно равносильно неравенству
|х³ − 5х + 2| ≥ x − 2,
которое заведомо удовлетворяется при x − 2 ≤ 0, т. е. при x ≤ 2. Пусть теперь x > 2. Разложим трехчлен на множители:
|х³ − 5х + 2| = |х³ − 4x − (x − 2)| = |x − 2| |х² + 2x − 1| = (x − 2)|х² + 2x − 1|.
Так как x > 2, то получаем равносильное неравенство
|х² + 2x − 1| ≥ 1,
а поскольку x² + 2x − 1 = x² + 2(x − ½) > 0, то
х² + 2x − 1 ≥ 1, или x² + 2(x − 1) ≥ 0.
Последнее неравенство удовлетворяется при любом x > 2.
Ответ. x − любое действительное число.
10.31. Так как x > 0, то вместо неравенства
![]()
можно написать
![]()
Если а > 1, то при логарифмировании по основанию а знак неравенства не изменится:
(logа x)² > 2,
откуда loga x < −√2, loga x > √2, т. е.
![]()
Если 0 < а < 1, то (loga x)² < 2 и
![]()
Ответ. При 0 < a < 1,
![]()
при а > 1,
![]()
x > a√2.
10.32. Если x > 0, то получаем неравенство, равносильное данному:
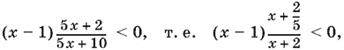
откуда 0 < x < 1.
Значение x = 0 удовлетворяет исходному неравенству. Если же x < 0, то непременно
5x + 2/5x + 10 =n,
где n — целое. Из условия x < 0 находим
x = 10n − 2/5 − 5n < 0,
откуда n < 1/5, n > 1, или n ≠ 1. Мы получили бесконечное множество значений x. Чтобы выбрать из них подходящие, разберем два случая, в зависимости от того, четное или нечетное число n. Когда n = 2k, данное неравенство можно переписать в виде |x|2k < 1, т. е. (|x| − 1)k < 0. Поскольку x < 0, то получаем (x + 1)k > 0. Так как x = 20k − 2/5 − 10k, то
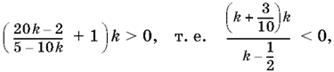
откуда k < −3/10, 0 < k < ½. Так как k — целое, то k = −1, −2, −3, ... . Получаем серию решений первоначального неравенства: x = 20k − 2/5 − 10k, k = −1, −2, −3, ... .
Пусть теперь n = 2k + 1. Тогда x = 10(2k + 1) − 2/5 − 5(2k + 1) = −10k + 4/5k. Так как x < 0, то исходное неравенство при этих значениях n удовлетворяется, если n ≠ 1, т. е. k ≠ 0.
Ответ. 0 ≤ x < 1, x = 20k − 2/5 − 10k, k = −1, −2, −3, ...; x = −10k + 4/5k, k = ±1, ±2, ±3, ... .
10.33. Данное неравенство эквивалентно неравенству
0 ≤ log2 3 − 2x/1 − x < 1.
(Ограничение слева обеспечивает неотрицательность числа, стоявшего под знаком квадратного корня.)
Поскольку 0 = log2 1, 1 = log2 2 и основание логарифмов больше единицы, последнее неравенство можно записать так:
1 ≤ 3 − 2x/1 − x < 2.
Требование положительности числа 3 − 2x/1 − x, которое могло быть нарушено при таком преобразовании, выполняется здесь автоматически.
Поскольку неравенство 1 ≤ y < 2 эквивалентно неравенству y − 1/y − 2 ≤ 0, получаем
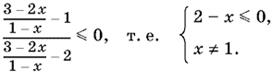
Ответ. x ≥ 2.
10.34. Данное неравенство равносильно системе
0 < |x − 1/2x + 1| < 1.
Тем самым мы обеспечили положительность числа, стоявшего в условии под знаком логарифма. Левое неравенство можно заменить условием x ≠ 1. Тогда получим систему
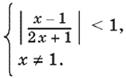
Эту систему можно преобразовать так:
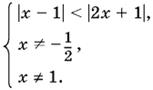
Входящее в эту систему неравенство можно возвести в квадрат, не нарушая его равносильности:
(x − 1)² < (2x + 1)²,
т. е. 3x² + 6х > 0, откуда x < −2, x > 0. Итак,
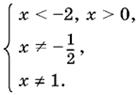
Ответ. x < −2, 0 < x < 1, x > 1.
10.35. Приведем все логарифмы, участвующие в неравенстве, к основанию 5:
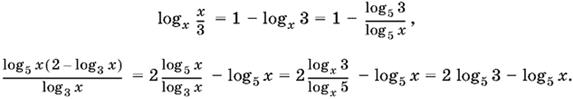
Последнее из преобразований правой части неравенства требует, вообще говоря, ограничения x ≠ 1. Однако это значение неизвестного оказывается «запретным», поскольку в левой части остается выражение, содержащее log5 x в знаменателе. Получаем равносильное неравенство
![]()
которое преобразуется к виду
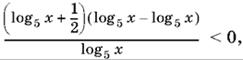
допускающему применение метода интервалов. Итак,
log5 x < −½, 0 < log5 x < log5 3.
Ответ. 0 < x < 1/√5, 1 < x < 3.
10.36. Так как log½ N = −log2 N, то данное неравенство перепишем в виде
log2 (2x − 1)log2 (2x + 1 − 2) < 2.
Преобразуем второй сомножитель:
log2 (2x + 1 − 2) = log2 [2(2x − 1)] = 1 + log2 (2x − 1).
Обозначив log2 (2x − 1) = y, получим квадратное неравенство
y(y + 1) < 2, или y² + y − 2 < 0,
решения которого лежат в интервале
−2 < y < 1.
Вспоминая, чему равен y, получим
−2 < log2 (2x − 1) < 1,
¼ < 2x − 1 < 2, 5/4 < 2x < 3.
Ответ. log2 5 − 2 < x < log2 3.
10.37. Преобразуем левую часть неравенства:
![]()
Неравенство
log|x + 6| (х² − x − 2) ≥ 1
равносильно совокупности двух систем
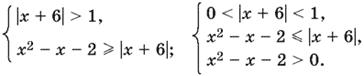
Второе неравенство первой системы равносильно совокупности систем решая которые найдем
x ≤ −2, x ≥ 4.
Таким образом, первая система может быть приведена к виду
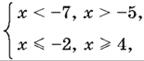
и ее решениями будут интервалы:
x < −7, −5 < x ≤ −2, x ≥ 4.
Решая второе неравенство второй системы, получим −2 ≤ x ≤ 4, а третье неравенство имеет решения x < −1, x > 2. Следовательно, система принимает вид
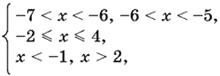
т. е. не имеет решений.
Ответ. x < −7, −5 < x ≤ −2, x ≥ 4.
10.38. Обозначим logа x = y. Неравенство примет вид
1 + y²/1 + y > 1.
Так как 1 + y² > 0, то и 1 + y > 0. Поэтому данное неравенство равносильно системе
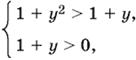
т. е.
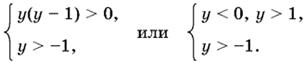
Получаем два интервала решений:
−1 < y < 0, y > 1.
Так как y = logа x, то нужно рассмотреть два случая.
Во−первых, если а > 1, то logа x − функция возрастающая и мы получим два интервала решений:
1/a < x < 1, x > а.
Если же 0 < а < 1, то получим другие два интервала решений:
1 < x < 1/a, 0 < x < а.
Ответ. При а > 1: 1/a < x < 1, x > а; при 0 < а < 1: 0 < x < а, 1 < x < 1/a.
10.39. Перейдем к основанию k:
![]()
где y = logk x. Последнее неравенство можно переписать так:
![]()
Выражение, стоящее в числителе, всегда положительно. Поэтому решением неравенства будут два интервала:
y < −1, y > 0.
Вспоминая, что y = logk x и 0 < k < 1, найдем соответствующие интервалы для x.
Ответ. 0 < x < 1, x > 1/k.
10.40. Поскольку 4x − 6 должно быть больше нуля, то x > 1. Следовательно, приходим к системе неравенств
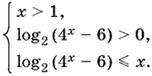
Решая второе неравенство системы, найдем x > log2 √7.
Третье неравенство перепишем в виде системы
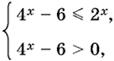
решением которой будет интервал log2 √6 < x ≤ log23. Так как log2 √7 > log2 √6, то получим решение данного неравенства.
Ответ. log2 √7 < x ≤ log2 3.
10.41. Данное неравенство эквивалентно такому:
![]()
Знаменатель всегда положителен. Поэтому
|х² − 4x| + 3 ≥ x² + |x − 5|,
остается раскрыть знаки абсолютной величины. Нанесем точки 0, 4, 5 на числовую ось и рассмотрим четыре случая.
Если x < 0, то получаем систему
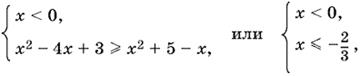
которой удовлетворяет полупрямая x ≤ −⅔.
Если 0 ≤ x ≤ 4, приходим к системе
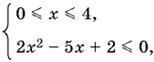
решением которой будет отрезок 1 < x < 2.
Если 4 < x ≤ 5, то наше неравенство примет вид x² − 4x + 3 ≥ x² + 5 − x, откуда x ≤ −⅔. Это не удовлетворяет условию 4 < x ≤ 5, а потому в данном случае решений нет.
Остается случай x > 5. Раскрывая знаки абсолютных величин, получим x ≤ 8/5. Здесь снова нет решений.
Ответ. x < −⅔; ½ ≤ x ≤ 2.
10.42. Из условия следует, что x > 2. Поэтому x³ − 7 > 0, а также x − 1 > 1 и (x − 1)² > 1. Данное неравенство равносильно такому:
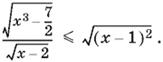
Так как x − 1 > 0, то
![]()
Поскольку x³ − 7/2 > 0, то ограничение x > 2 достаточно для того, чтобы следующие преобразования приводили к равносильным неравенствам:
![]()
После упрощений последнее неравенство сведется к квадратному: −4x² + 5x + 3/2 ≥ 0, имеющему решения −¼ < x < 3/2. Так как, кроме того, x > 2, то исходное неравенство не имеет решений.
Ответ. Решений нет.
10.43. Так как первый сомножитель положителен, то, чтобы неравенство удовлетворялось, необходимо
log2 (2 − 2x²) > 0, т. е. 2 − 2x² > 1, √2|x| < 1,
откуда
0 ≤ √2|x| < 1 и −1 ≤ √2|x| − 1 < 0.
Следовательно, |√2|x| − 1| ≤ 1. Таким образом, первоначальное неравенство может удовлетворяться только, если
log2 (2 − 2x²) ≥ 1, или 2 − 2x² ≥ 2, −x² ≥ 0,
т. е. x = 0. Проверкой убеждаемся, что x = 0 является решением неравенства.
Ответ. x = 0.
10.44. Так как
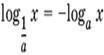
, то перепишем неравенство следующим образом:
![]()
Обозначив log3 x + 1/x − 1 = y, получим log2 y < 0, откуда
0 < y < 1, т. е. 0 < log3 x + 1/x − 1 < 1,
а потому 1 < x + 1/x − 1 < 3.
Последнее неравенство можно записать так:
(x + 1/x − 1 − 1)(x + 1/x − 1 − 3) < 0
(если некоторое выражение заключено между двумя числами, то разности между ним и каждым из этих чисел имеют разные знаки).
После выполнения действий в скобках и небольших упрощений получим
x − 2/(x − 1)² > 0,
откуда x > 2.
Ответ. x > 2.
10.45. Если 0 < x² − 1 < 1, то придем к системе
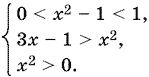
Так как последнее неравенство следует из первого, то получаем такую систему:

откуда 1 < x < √2.
Если x² − 1 > 1, т. е. x² > 2, то приходим ко второй системе:
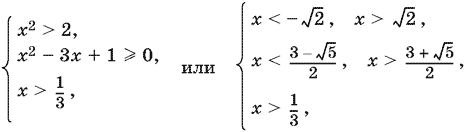
откуда x > 3 + √5/2.
Ответ. 1 < x < √2, x > 3 + √5/2.
10.46. Перепишем неравенство в виде
![]()
Равносильность при этом не нарушается, так как оба выражения в квадратных скобках (полученное и данное в условии) существуют одновременно при x > 0. Выясним, когда основание положительно и когда оно отрицательно (если оно равно нулю, то неравенство не удовлетворяется). Для этого воспользуемся условным символом V, обозначающим сравнение левой и правой частей, и не будем нарушать равносильность при преобразованиях:
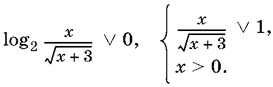
Преобразуем первое соотношение, имея в виду, что x − положительное число:
![]()
Итак, при
![]()
основание положительно, а при
![]()
оно отрицательно. Из отрицательных значений основания мы должны рассмотреть лишь те, при которых x − 4, а следовательно и x, — четное число. Среди чисел, заключенных в интервале
![]()
, есть только одно четное: x = 2. Подставим это число в левую часть исходного неравенства:
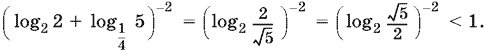
Таким образом, x = 2 не удовлетворяет данному неравенству.
Пусть теперь основание положительно, т. е.
![]()
. Тогда неравенство (1) равносильно такому:
![]()
т. е.
![]()
(пояснения приведены во втором указании на с. 192). В последнем неравенстве основание степени положительно, так как x > 0. Следовательно, его можно преобразовать к виду
![]()
т. е.
![]()
Мы рассматриваем случай
![]()
. Решив неравенства
![]()
получим, что выражение
![]()
больше нуля, когда x > 6, равно нулю, когда x = 6, и меньше нуля, когда
![]()
Таким образом, вместо неравенства (2) можно записать
(x − 6)(x − 4) ≥ 0,
т. е.
![]()
Ответ.
![]()
10.47. Данное неравенство может выполняться только в том случае, если дискриминант стоящего в левой части квадратного трехчлена относительно x положителен, т. е.
![]()
Решением этого неравенства будут
log0,5 y² < −3, log0,5 y² > 1.
В первом случае получим y² > 8, во втором 0 < y² < ½.
Ответ. y < −√8, −1/√2 < y < 0, 0 < y < 1/√2, y > √8.
10.48. Для ответа на вопрос задачи нужно найти такие значения а, что множество решений второго неравенства не у́же множества решений первого. Таким образом, если y первого неравенства есть решения, они все должны попасть в интервал (−3, −1).
Корнями квадратного трехчлена
х² − а(1 + а²)x + а4
будут числа а и а³. Когда они совпадают (а = ±1, а = 0), ветви параболы направлены вверх и квадратный трехчлен не может стать отрицательным.
Докажем, что следствием неравенства, не имеющего решений, является любое неравенство. В частности, любое решение первого неравенства при а = 0, ±1 содержится среди решений второго. Предположим, что это не так. Тогда существует решение первого неравенства, не удовлетворяющее второму. Мы приходим к противоречию с тем фактом, что первое неравенство в рассматриваемых случаях вообще не имеет решений.
Если же корни различны (а ≠ а³), то оба они должны попасть в интервал [−3, −1]
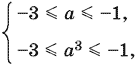
т. е.
![]()
Ответ.
![]()
10.49. Сначала решим строгое неравенство
![]()
Оно равносильно системе

При а ≤ 1 решений y этой системы нет. При а > 1 ее решениями будут значения x, для которых 1 < x < а.
Остается выяснить, какие значения x удовлетворяют уравнению
![]()
(4)
Это уравнение равносильно совокупности двух систем:
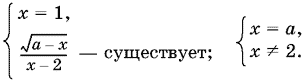
Поскольку в первой системе x = 1, то x ≠ 2; остается обеспечить, чтобы а − 1 ≥ 0, т. е. а ≥ 1.
Итак, при каждом а ≥ 1 есть решение x = 1, а при каждом x ≠ 2 есть решение x = а. (При а = 1 эти решения совпадают.)
Решение второй системы при а ≠ 2: x = а. Остается объединить решения неравенства (3) и уравнения (4).
Ответ. При а ≤ 1 имеем x = а; при 1 < а < 2 имеем 1 ≤ x ≤ а; при а = 2 имеем 1 ≤ x < 2; при а > 2 имеем 1 ≤ x ≤ 2, x = а.
10.50. Поскольку
х² + 8х + 15 = (x + 3)(x + 5), а x² + 7х + 10 = (x + 2) (x + 5),
то данное неравенство можно записать в виде
(x + 5)[(x + 3) · 22 + x − (2 + x)] > 0. (5)
При x + 5 = 0 исходное неравенство не удовлетворяется. Поэтому (5) равносильно совокупности двух систем:
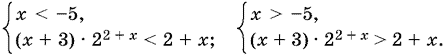
Далее придется рассмотреть случаи x + 3 < 0 и x + 3 > 0 (при x + 3 = 0 неравенство (3) удовлетворяется!). Располагая точки x = −5 и x = −3 на числовой оси, мы получим три интервала x < −5; −5 < x < −3; x > −3. Соответственно, приходим к совокупности трех систем неравенств:
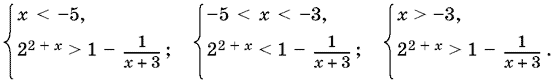
Построим графики функций
y1 = 22 + x, y2 = 1 − 1/x + 3
(рис. P.10.50).
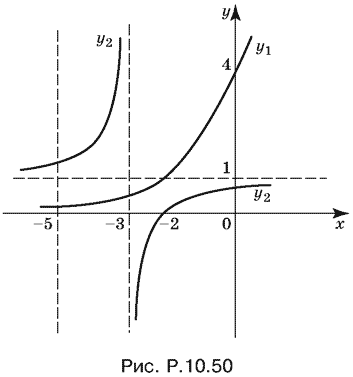
Просто сослаться на график и указать интервалы решений нельзя. График подскажет, какие сравнения нужно привести для решения неравенства.
При всех x < −5 получим, что y2 > 1, а y1 < 1, т. е. y1 < y2: второму неравенству первой системы значения x < −5 не удовлетворяют.
При −5 < x < −3 также y1 < 1, а y2 > 1 и снова y1 < y2. Однако на этот раз второе неравенство второй системы удовлетворяется.
При x > −3 второе неравенство третьей системы вновь удовлетворяется. В самом деле, при −3 < x < −2, y1 > 0, а y2 < 0, т. е. y1 > y2. Далее при x ≥ −2 имеем у1 ≥ 1, 0 < y2 < 1, т. е. снова у1 > y2. Остается вспомнить, что x = −3 было решением (5).
Ответ. x ∈ (−5; +∞).
10.51. Ясно, что подставлять интересующие нас значения x в данное неравенство и проверять, удовлетворяется ли это, не нужно. Проще это неравенство решить. Так как lg 5 ≠ ½, то |0,5 − lg 5| > 0, т. е.
![]()
Любое число а ^ 0 можно записать в виде а = |а| sign а, где
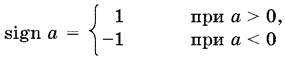
— функция, соответствующая знаку числа а. Поэтому из (6) получаем
![]()
Определим теперь знак выражения
0,5 − lg 5 = lg √10 − lg 5 = lg √10/5 < lg 4/5 < lg 1 = 0.
Следовательно, sign (0,5 − lg 5) = −1, т. е. решением неравенства (6) будут значения x ≤ −1.
Ответ. −4, −1.
10.52. Так как (√5 + 2)(√5 − 2) = 1, то данное неравенство можно преобразовать к виду
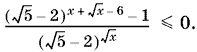
(7)
Знаменатель всегда положителен, если x ≥ 0. Требование x ≥ 0 сохраняется, если существует числитель. Поэтому (7) равносильно неравенству
(√5 − 2) x + √x − 6 ≤ 1. (8)
Поскольку 0 < √5 − 2 < 1, то (8) равносильно неравенству
x + √x − 6 ≥ 0. (9)
Трехчлен y² + y − 6 (где y = √x) имеет корни −3 и 2. Поэтому решением неравенства
y² + y − 6 ≥ 0
будет совокупность значений y ≤ −3, y ≥ 2. У неравенства √x ≤ −3 решений нет. Остается √x ≥ 2, т. е. x ≥ 4.
Ответ. [4, +∞).
10.53. Обозначим log2x = y и запишем неравенство в виде
1 + y² ≤ |y| (4x − x² − 2),
или
1 + y² ≤ |y| [−(x² − 4x + 4) + 2],
т. е.
1 − 2|y| + |y²| ≤ |y|(−x² + 4x − 4).
Итак,
(1 − |y|)² ≤ −|y|(x − 2)².
Неравенство удовлетворяется только в том случае, если обе его части равны нулю. Это может быть только при |y| = 1, тогда (x − 2)² ≤ 0, т. е. x = 2.
Ответ. 2.