Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Логарифмические и показательные уравнения и системы
11.1.
![]()
11.2. Так как 1225 = 35², то
lg 122,5 = lg 35² − lg 10 = 2(lg 5 + lg 7) − 1 = 2(а + b) − 1.
11.3. Перепишем уравнение в виде
![]()
т. е. после того как вынесем 32x − 1 и 2x + ½ за скобки,
![]()
Из последнего уравнения следует, что
32x − 3 = (√2)2x − 3,
т. е. (3/√2)2x − 3 = 1, откуда 2x − 3 = 0.
Ответ. x = 3/2.
11.4. Обозначив 3−|x − 2| = y, придем к квадратному уравнению
y² − 4y − а = 0,
корни которого
![]()
Первый корень
![]()
приходится отбросить, так как −|x − 2| ≤ 0 и 3−|x − 2| ≤ 1, а
![]()
не может стать меньше двух.
Исследуем второй корень:
![]()
Чтобы это уравнение имело решение, необходимо выполнение трех условий, которые сведены в систему неравенств:
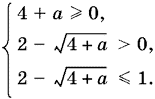
Решая эту систему, найдем −3 ≤ а < 0.
Ответ. При −3 ≤ а < 0 два решения:
![]()
при остальных а решений нет.
11.5. Решая квадратное уравнение относительно 12|x|, найдем
![]()
Первое ограничение: 1 − а ≥ 0, т. е. а ≤ 1. Кроме того, 12|x| не может стать меньше единицы. Если перед корнем выбран знак плюс, то последнее требование выполняется, если же взят знак минус, то
![]()
лишь при а = 1. Это значение а можно учесть при рассмотрении уравнения
![]()
Ответ.
![]()
при а ≤ 1; при остальных а решений нет.
11.6. Уравнение можно записать так:
![]()
или
![]()
Прологарифмируем по основанию 10
![]()
откуда x1 = 2, x2 = −1/lg 5.
Ответ. 2, −1/lg 5.
11.7. Так как (2 + √3)(2 − √3) = 1, то 2 + √3 и 2 − √3 — взаимно обратные числа. Обозначим
(2 + √3)x² − 2x = y.
Тогда данное уравнение можно записать так:
y + 1/y = 101/10
(мы разделили обе части уравнения на 2 + √3).
Решая это уравнение, найдем
y1 = 1/10, y2 = 10.
Покажем, что первый корень, который приводит к уравнению
(2 + √3)x² − 2x = 1/10,
посторонний.
Так как 2 + √3 > 1, то x² − 2x < 0. Выражение x² − 2x достигает своего минимума в точке x = 1. Этот минимум равен −1. Поскольку 2+ √3 < 4, то в левой части последнего уравнения стоит число, большее ¼, а следовательно, ни при каких x не равное 1/10.
Остается решить уравнение
(2 + √3)x² − 2x = 10.
Прологарифмируем его по основанию 2 + √3:
x² − 2x − log2 + √3 10 = 0.
Ответ.
![]()
11.8. Перепишем уравнение так:
![]()
Сразу же видно, что x = 2 — корень уравнения. Покажем, что других корней нет.
Обозначим для удобства первое основание через а, а второе через b. Оба этих основания меньше единицы. Поэтому
b < а < 1;
если x < 2, то аx > а², bx > b², и следовательно,
аx + bx > 1;
если же x > 2, то аx < а², bx < b², и следовательно, аx + bx < 1.
Ответ. x = 2.
11.9. Если x − 2 ≠ 0, 1, −1, то log2 (x + 31) = 3, x = −23. При x = 2 = 0, т. е. x = 2, имеем
![]()
, и так как log231 > 0, то уравнение удовлетворяется.
При x − 2 = 1, т. е. x = 3, уравнение также удовлетворяется.
Если x − 2 = −1, т. е. x = 1, имеем
![]()
Остается проверить значение x = −23. Тогда log2 8 = 3, и уравнение снова удовлетворяется.
Ответ. −23, 1, 2, 3.
11.10. Так как log3 (3x + 1 − 3) = 1 + log3 (3x − 1), то, обозначив log3 (3x − 1) через y, получим
y² + y − 6 = 0,
откуда y1 = −3, y2 = 2.
Если log3 (3x − 1) = −3, то 3x = 28/27 и x1 = log3 28 − 3. Если log3 (3x − 1) = 2, то 3x = 10 и x2 = log3 10.
Ответ. log3 28 − 3, log3 10.
11.11. Перепишем уравнение в виде
log7 x + logx 7 = log²7 x + log²x 7 − 7/4.
Дополним правую часть его до полного квадрата суммы (заметим, что log7 x · logx 7 = 1) и обозначим
log7 x + logx 7 = y.
Получим уравнение:
4у² − 4у − 15 = 0, откуда у1 = 5/2, y2 = −3/2.
Если logx 7 + log7 x = 5/2, то
![]()
Если же logx 7 + log7 x = −3/2, то получим уравнение
![]()
y которого нет действительных корней.
Ответ. x1 = 49, x2 = √7.
11.12. Прологарифмируем по основанию 3 и перейдем к общему основанию логарифмов:
![]()
откуда следует уравнение
y³ − 2y + 1 = 0,
где y = log3 x.
Так как у³ − 2y + 1 = (y − 1)(y² + y − 1), то
y1 = 1, y2,3 = −1 ± √5/2.
Находим соответствующие x и проверяем их.
Ответ. x1 = 3, x2,3 = 3.
11.13. Если
y = logх 3,
то придем к уравнению
![]()
из которого получается цепочка следствий
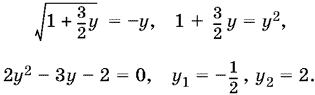
Проверкой убеждаемся, что второе значение y не удовлетворяет исходному уравнению, так как y должен быть отрицательным.
Ответ. x = 1/9.
11.14. Приведя уравнение к общему знаменателю и отбросив его, получим следствие данного уравнения:
log4 x + log4(10 − x) = 2,
откуда
x² − 10x + 16 = 0, x1 = 2, x2 = 8.
Проверкой убеждаемся, что это — корни исходного уравнения.
Ответ. x1 = 2, x2 = 8.
11.15. Перепишем данное уравнение так:
![]()
При этом преобразовании мы могли потерять корень, так как при x = 1 левая часть полученного уравнения теряет смысл, в то время как обе части исходного уравнения существуют. Проверкой убеждаемся, что x = 1 — корень данного уравнения[21].
Преобразуем выражения, стоящие в знаменателях и обозначим logx 2 = y:
1/1 − y − 21/4y + 1 + 10/2y + 1 = 0.
Это уравнение равносильно системе
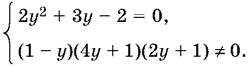
При y = −2 и y = ½, являющихся корнями уравнения, условие, входящее в систему, удовлетворяется.
Ответ. x1 = 1, x2 = 1/√2, x3 = 4.
11.16. Перепишем уравнение в виде
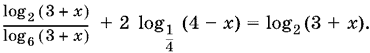
Так как
![]()
то придем к уравнению
log2 6 − log2 (4 − x) = log2 (3 + x),
откуда
х² − x − 6 = 0, x1 = −2, x2 = 3.
Все применявшиеся преобразования приводили к следствию исходного уравнения. Первый корень при проверке отбрасываем, так как
![]()
при x = −2 не существует.
Ответ. x = 3.
11.17. Уравнение равносильно системе
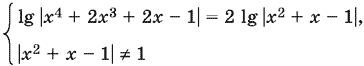
или
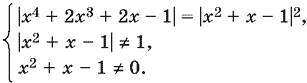
Решим уравнение, после чего проверим, выполняются ли наши ограничения. Уравнение распадается на два. Если
x4 + 2x³ + 2x − 1 = (х² + x − 1)²,
то, раскрывая скобки, получим
х² + 4x − 2 = 0, x1,2 = −2 ± √6.
Если же
x4 + 2x³ + 2x − 1 = −(х² + x − 1)²,
то
x²(2x² + 4x − 1) = 0; x3 = 0, x4,5 = −2 ± √6/2.
Остается проверить выполнение двух условий, входящих в последнюю систему. Лишь при x = 0 нарушается условие |х² + x − 1| ≠ 1. При остальных найденных значениях x оба условия выполняются.
Ответ. x1,2 = −2 ± √6; x3,4 = −2 ± √6/2.
11.18. Преобразуем первое слагаемое:
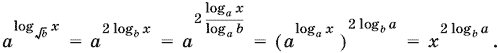
При переходе к логарифмам с основанием а мы наложили на а дополнительное ограничение: а ≠ 1. Однако при а = 1 данное нам уравнение не имеет решений, и, следовательно, такое ограничение несущественно. При замене
![]()
на x могут быть введены посторонние корни x < 0.
Мы получили уравнение относительно
![]()
:
y² − 5у + 6 = 0; y1 = 2, y2 = 3,
откуда
![]()
Ответ. При
![]()
11.19. Логарифмируя и заменяя logx а на
![]()
, получим
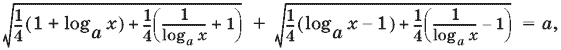
т. е.
![]()
Отсюда видно, что если x удовлетворяет этому уравнению, то loga x > 0, а потому loga x + 1 > 0. Следовательно,
![]()
Чтобы разбирать меньшее количество различных случаев, оценим левую часть последнего уравнения и, следовательно, а. Так как
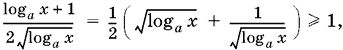
а второе слагаемое неотрицательно, то а > 1 (значение а = 1 мы исключили, так как а — основание логарифма). Остается рассмотреть случаи, позволяющие раскрыть символ абсолютной величины.
При loga x ≥ 1, т. е. при x ≥ а > 1, получим уравнение
![]()
Так как а > 1, то x > а.
При 0 < loga x < 1, т. е. при x < а, получим второе значение неизвестного:
![]()
которое будет меньше а, так как а > 1.
Ответ. При
![]()
11.20. Если одно из неизвестных равно нулю, то в силу второго уравнения системы равно нулю и второе неизвестное. Это приводит к потере смысла в первом уравнении. Таким образом, x и y оба положительны.
Прологарифмируем оба уравнения:
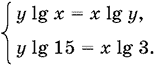
Так как x > 0 и y > 0, то разделим первое уравнение на второе:
![]()
а потому
![]()
Подставим найденное значение x в первое из данных уравнений:
![]()
Если y = 1, то из первого уравнения системы получаем x = 1, что не удовлетворяет второму уравнению.
Так как значения y = 0 и y = −1 исключены, то остается
![]()
Вспомнив, что log3 15 = 1 + log3 5, получим
![]()
и найдем x.
Ответ.
![]()
11.21. Возведем второе уравнение в степень y
1024 = (2x/3)2y
и воспользуемся тем, что xy = 243. Так как 1024 = 210, а 243 = 35, то получим
210 = (⅔)2y · 310, откуда (⅔)10 = (⅔)2y
и y = 5. Из первого уравнения находим x = 3.
Делаем проверку и убеждаемся, что мы нашли решение системы.
Ответ. (3, 5).
11.22. Из самого вида системы следует, что x > 0, y > 0. Из второго уравнения имеем
![]()
а после подстановки в первое
![]()
Если y ≠ 1 (случаи y = 0 и y = −1 уже исключены), то, приравнивая показатели степеней, получим
![]()
Подставляя в первое уравнение, найдем
![]()
Следовательно,
![]()
откуда получаем x1 = 16/81, у1 = 4/9. Проверкой убеждаемся, что это — решение исходной системы.
Остается проверить, что произойдет при y = 1. Легко видеть, что тогда и x = 1.
Ответ. (16/81, 4/9), (1, 1).
11.23. Так как
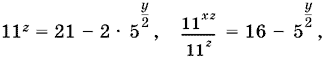
то
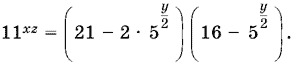
Подставив в первое уравнение исходной системы и обозначив
![]()
получим
(21 − 2u)(16 − u) − 2u³ = 71,
а после раскрытия скобок
u = 5, т. е. y = 2.
Остальные неизвестные находятся легко.
Ответ. (2, 2, 1).
11.24. Второе уравнение можно записать в виде
2x + 2у (x · 2x − y + 1 + 3y · 22x + y) = 1.
В силу первого уравнения системы выражение в скобках равно 2. Поэтому
2x + 2у + 1 = 1,
откуда
x + 2y + 1 = 0, т. е. x = −2y − 1.
После подстановки в первое уравнение системы получим
2−3y − 3 = 1/−4 − 5y, или 23(y + 1) = −(4 + 5y).
Чтобы это уравнение имело решение, необходимо выполнение неравенства
−(4 + 5у) > 0, т. е. y < −4/5.
Рассмотрим следующие три случая.
1. 3(y + 1) < 0, т. е. y < −1. В этом случае правая часть уравнения должна быть меньше единицы, т. е. −(4 + 5у) < 1, откуда y > −1. Поскольку ограничения y < −1 и y > −1 несовместны, при сделанном предположении нет решений.
2. 3(y + 1) > 0, т. е. y > −1. Тогда правая часть уравнения должна превзойти единицу, а потому y < −1. И на этот раз ограничения несовместны.
3. Остается посмотреть, что будет при 3(y + 1) = 0, т. е. y = −1. Легко проверить, что уравнение удовлетворяется. Найденному значению y соответствует x = 1. Проверкой убеждаемся, что мы нашли решение исходной системы.
Ответ. (1, −1).
11.25. Первое уравнение системы можно переписать в виде
log8 (y − x)³ = log8 (3y − 5х).
Следствием данной системы является система
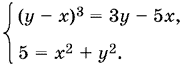
Перемножив входящие в нее уравнения, получим однородное уравнение относительно x и y:
5(y − x)³ = (3y − 5х)(х² + y²).
Если x ≠ 0, то разделим последнее уравнение почленно на x³ и обозначим y/x = u. Получим уравнение относительно u:
u³ − 5u² + 6u = 0,
которое имеет корни: u1 = 0, u2 = 2, u3 = 3.
Если u = 0, то y = 0, а из второго уравнения исходной системы x = ±√5.
При подстановке в первое уравнение исходной системы x = −√5 и y = 0 это уравнение удовлетворяется, а при x = √5 и y = 0 уравнение не удовлетворяется. Если u = 3, то y = 3x, а потому x² = ½, откуда
x =±1/√2, y = ±3/√2
(x и y в силу равенства y = 3x имеют одинаковые знаки). Подстановкой в первое уравнение убеждаемся, что решением системы будут
x = 1/√2, y = 3/√2.
Если u = 2, то y = 2x. Из двух систем значений (−1, −2), (1, 2) первому уравнению удовлетворяет только вторая.
Осталось рассмотреть случай x = 0. Он не дает новых решений, так как система превращается в два несовместных уравнения.
Ответ. (−√5, 0); (1/√2, 3/√2); (1, 2).
11.26. Способ 1. Из второго уравнения
![]()
Подставляем в первое:
![]()
Так как
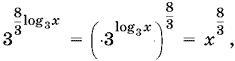
то получим уравнение
![]()
Прологарифмируем по основанию 3:
3log3² x − 8log3 x + 4 = 0,
откуда x1 = 3⅔, x2 = 9.
Находим соответствующие y и делаем проверку.
Способ 2. Применим равенство
![]()
(оно доказывается с помощью логарифмирования) к первому уравнению. Получим
![]()
т. е.
![]()
или
![]()
Прологарифмировав по основанию 3, решим полученное уравнение совместно со вторым уравнением системы:
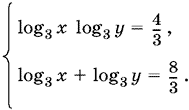
Ответ.
![]()
11.27. Так как x и y одного знака (это следует из второго уравнения) и x + y > 0 (из первого), то x и y положительны, причем либо x, либо y обязательно больше 1 (так как xy = 3). Следовательно, x + y > 1 и данная система может быть переписана так:
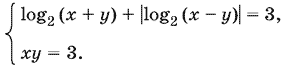
Если 0 < x − y < 1, то получим систему
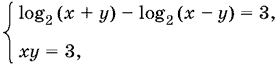
следствием которой является система
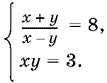
Из первого уравнения получим 7 x = 9y. Подставляя сюда y = 3/x, найдем x² = 27/7, откуда
![]()
Убеждаемся, что при этих значениях x и y неравенство 0 < x − y < 1 выполняется.
Если x − y > 1, то получим систему
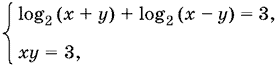
следствием которой является система
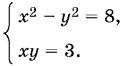
Подставляя в первое уравнение y = 3/x, получим уравнение
x4 − 8x² − 9 = 0.
Так как x² ≠ −1, то остается x² = 9, откуда x = 3, а y = 1. (Ограничение x − y > 1 удовлетворяется.)
Равносильность могла быть нарушена только при потенцировании; поэтому достаточно проверить, что x − y > 0, что уже сделано.
Ответ.
![]()
11.28. Прологарифмируем и обозначим log2 x = u, log2 (y + 1) = u:
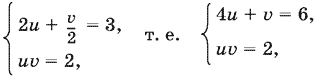
откуда
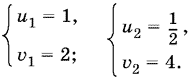
Находим соответствующие x и y; проверка не обязательна, так как равносильность не была нарушена.
Ответ. (√2, 15); (2, 3).
11.29. Так как loga² x = ½ loga x (обратите внимание на то, почему мы не пишем здесь log|a| x), а log√b √y = logb y, то систему можно переписать следующим образом:
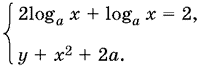
Это — следствие первоначальной системы; если же добавить условия y > 0, b > 0, b ≠ 1, то получим равносильную систему.
Из первого уравнения
![]()
Подставляем во второе и находим
![]()
Условие
![]()
, т. е. 8а³ > а4, приводит к дополнительному ограничению на а: а < 8.
Ответ. При 0 < а < 1, 1 < а < 8 и при b > 0, b ≠ 1
![]()
![]()
11.30. Пусть 3x + 1 = u, 3y + z − x = v, тогда первые два уравнения примут вид
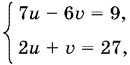
откуда u = 9, v = 9. Следовательно, x = 1, а y + z − x = 2, т. е. y + z = 3. Последнее уравнение данной системы примет теперь простой вид
lg уz = lg 2,
следствием которого будет
уz = 2.
Решаем систему
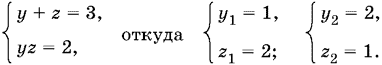
Проверкой убеждаемся, что мы нашли решения исходной системы уравнений.
Ответ. (1, 1, 2); (1, 2, 1).